
3.下列关于地理环境对其它生产活动影响的叙述,不正确的是 ( )
A.长江三角洲的轻工业发展依托于当地发达的农业基础
B.长江三角洲发展重工业依托于当地丰富的矿产资源
C.松嫩平原发展重化工业依托于当地丰富的石油资源和周围地区的煤、铁等资源
D.长江三角洲商业贸易发达依托于优势的地理位置
2.关于长江三角洲和松嫩平原共性的叙述,正确的是 ( )
①都位于平原地区 ②都位于我国的东部季风区
③都位于第三阶梯 ④雨热同期
A.①②③ B.②③④ C.①③④ D.①②③④
1.下列关于区域特征的叙述,正确的是 ( )
A.区域有明显的界线
B.区域不一定具有优势、特色和功能
C.区域内部有显著的差异
D.区域之间是相互联系的
在学习实数与向量的积的运算律时,应启发学生寻求其与代数运算中实数乘法的运算律的相似性,但应注意它们之间的区别,从而掌握实数与向量的积及其应用.
4.设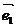 ,
, 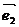 是两个不共线向量,已知
是两个不共线向量,已知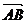 =2
=2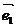 +k
+k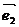 ,
, 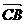 =
=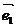 +3
+3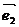 ,
, 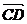 =2
=2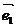 -
-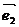 , 若三点A,
B, D共线,求k的值
, 若三点A,
B, D共线,求k的值
解: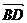 =
=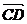 -
-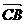 =(2
=(2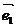 -
-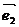 )-(
)-(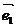 +3
+3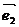 )=
)=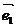 -4
-4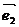
∵A, B, D共线 ∴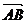 ,
,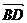 共线 ∴存在λ使
共线 ∴存在λ使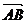 =λ
=λ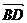
即2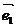 +k
+k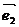 =λ(
=λ(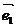 -4
-4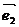 ) ∴
) ∴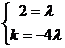 ∴k=-8
∴k=-8
3.在 
 ABCD中,设对角线
ABCD中,设对角线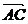 =
= ,
,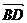 =
= 试用
试用 ,
,  表示
表示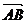 ,
,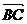
 解法一:
解法一: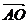 =
=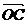 =
=

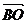 =
=
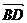 =
=

∴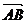 =
=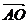 +
+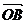 =
=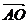 -
-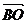 =
=
 -
-

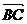 =
=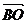 +
+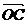 =
=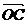 +
+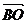 =
=
 +
+

解二:设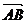 =
=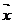 ,
,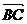 =
=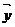
则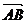 +
+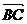 =
=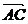 ,即
,即 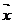 +
+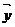 =
= ;
;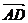 -
-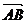 =
=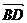 ,即
,即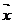 -
-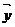 =
=
∴ 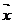 =
= (
( -
- ),
), 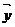 =
= (
( +
+ )
)
即 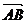 =
= (
( -
- )
) 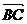 =
= (
( +
+ )
)
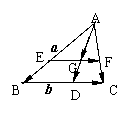
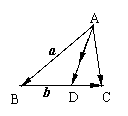
2.如图,在△ABC中,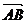 =
= ,
, 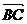 =
= ,AD为边BC的中线,G为△ABC的重心,求向量
,AD为边BC的中线,G为△ABC的重心,求向量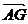
 解法一:∵
解法一:∵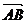 =
= ,
, 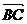 =
= 则
则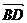 =
=
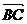 =
=

∴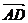 =
=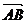 +
+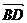 =
= +
+
 而
而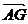 =
=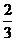
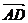
∴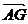 =
=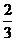
 +
+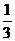

解法二:过G作BC的平行线,交AB、AC于E、F
∵△AEF∽△ABC,
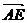 =
=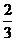
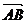 =
=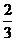

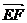 =
=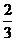
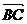 =
=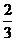

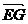 =
=
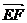 =
=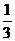

∴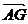 =
=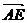 +
+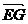 =
=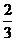
 +
+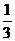

1.当λÎZ时,验证:λ( +
+ )=λ
)=λ +λ
+λ
证:当λ=0时,左边=0•( +
+ )=
)=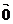 右边=0•
右边=0• +0•
+0• =
=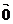 分配律成立
分配律成立
当λ为正整数时,令λ=n,
则有:n( +
+ )=(
)=( +
+ )+(
)+( +
+ )+…+(
)+…+( +
+ )
)
= +
+ +…+
+…+ +
+ +
+ +
+ +…+
+…+ =n
=n +n
+n
即λ为正整数时,分配律成立
当为负整数时,令λ=-n(n为正整数),有
-n( +
+ )=n[-(
)=n[-( +
+ )]=n[(-
)]=n[(- )+(-
)+(- )]=n(-
)]=n(- )+n(-
)+n(- )=-n
)=-n +(-n
+(-n )=-n
)=-n -n
-n
分配律仍成立
 综上所述,当λ为整数时,λ(
综上所述,当λ为整数时,λ( +
+ )=λ
)=λ +λ
+λ 恒成立
恒成立 
2.用向量法解决几何问题
向量是数学中重要概念之一,是解决数学问题的得力工具,它简洁明快,许多几何里的命题,如果用向量知识来解决就显得格外简练.
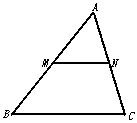 如图,MN是△ABC的中位线,求证:MN=
如图,MN是△ABC的中位线,求证:MN= BC,且MN∥BC.
BC,且MN∥BC.
证明:∵M、N分别是AB、AC边上的中点,所以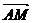 =
=
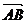 ,
,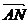 =
=
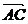 ,
,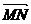 =
=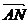 -
-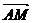 =
=
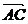 -
-
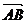 =
= (
(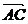 -
-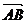 )=
)=
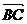 .
.
因此,NM= BC且MN∥BC.
BC且MN∥BC.
1.错例分析
判断向量a=-2e与b=2e是否共线?
对此题,有同学解答如下:
解:∵a=-2e,b=2e,∴b=-a,∴a与b共线.
分析:乍看上述解答,真是简单明快.然而,仔细研究题目已知,却发现
其解答存有问题,这是因为,原题已知中对向量e并无任何限制,那么就应允许e=0,而当e=0时,显然a=0,b=0,此时,a不符合定理中的条件,且使b=λa成立的λ值也不惟一(如λ=-1,λ=1,λ=2等均可使b=λa成立),故不能应用定理来判断它们是否共线.可见,对e=0的情况应另法判断才妥.
综上分析,此题应解答如下:
解:(1)当e=0时,则a=-2e=0
由于“零向量与任一向量平行”且“平行向量也是共线向量”,所以,此时a与b共线.
(2)当e≠0时,则a=-2e≠0,b=2e≠0
∴b=-a(这时满足定理中的a≠0,及有且只有一个实数λ(λ=-1),使得b=λa成立)
∴a与b共线.
综合(1)、(2)可知,a与b共线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com