能力目标:通过对一道教材例题的“先探究--再创造教学.培养学生“归纳与猜想 .“探索与发现的能力,——青夏教育精英家教网—

0 423638 423646 423652 423656 423662 423664 423668 423674 423676 423682 423688 423692 423694 423698 423704 423706 423712 423716 423718 423722 423724 423728 423730 423732 423733 423734 423736 423737 423738 423740 423742 423746 423748 423752 423754 423758 423764 423766 423772 423776 423778 423782 423788 423794 423796 423802 423806 423808 423814 423818 423824 423832 447090

2、能力目标：通过对一道教材例题的“先探究--再创造”教学，培养学生“归纳与猜想”、“探索与发现”的能力；

试题详情

[研究目标]

本节课是一节探究课。如何让学生在学习过程中不再是单纯地做题训练，而是通过探究，亲历数学知识产生和发展过程，体验数学发现和创造的历程，使学生的学习过程，真正成为在教师的引导下的探究与再创造过程，是本节研究课的研究目标。

[研究策略]

为了实现研究目标，我采取的策略是：“先探究--再创造”，具体做法如下：

尝试变换--提出问题：利用从特殊到一般循序渐进原则，激活学生的思考热情

观察探究--研究问题，利用独立思考和创造性原则，让学生经历思考过程

　　推理论证--揭示问题，探索解决数学问题的思维过程，有效提升思考质量

[教学目标]

1、知识目标：会正确解决直线与抛物线的有关问题；

试题详情

2. (或)的参数方程为(或)(为参数).

　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
抛物线
例21. 顶点在原点，焦点是的抛物线方程是(　 )
(A)x²=8y　　　　　 (B)x²= -8y　　　　 (C)y²=8x 　　　　　(D)y²= -8x
例22. 抛物线上的一点到焦点的距离为1，则点的纵坐标是(　　 )
(A)　　　　　　　 (B)　　　　　　　 (C)　　　　　　　 (D)0
例23.过点P(0,1)与抛物线y²=x有且只有一个交点的直线有(　 )
(A)4条　　　　　　 (B)3条　　　　　　 (C)2条　　　　　　 (D)1条
例24. 过抛物线(a>0)的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别为p、q，则等于(　 )
(A)2a　　　　　　　(B)　　　　　　　(C)　　　　　　(D)
例25. 若点A的坐标为(3，2)，F为抛物线y²=2x的焦点，点P在抛物线上移动，为使|PA|+|PF|取最小值，P点的坐标为(　　 )
(A)(3，3) 　　　　　(B)(2，2)　　　　　　(C)(，1)　　　　　　(D)(0，0)
例26. 动圆M过点F(0，2)且与直线y=-2相切，则圆心M的轨迹方程是　　　　　　　 .
　
例27. 过抛物线y²＝2px的焦点的一条直线和抛物线交于两点，设这两点的纵坐标为y₁、y₂，则y₁y₂＝_________.
例28. 以抛物线的焦点为圆心，通径长为半径的圆的方程是_____________.
　
例29. 过点(-1,0)的直线l与抛物线y²=6x有公共点，则直线l的倾斜角的范围是　　　　　　　　 .
　
例30设是一常数，过点的直线与抛物线交于相异两点A、B，以线段AB为直经作圆H(H为圆心)。
(Ⅰ)试证:抛物线顶点在圆H的圆周上；
(Ⅱ)求圆H的面积最小时直线AB的方程.
　
　
　
轨迹
问题
上一章已经复习过解析几何的基本问题之一：
如何求曲线(点的轨迹)方程,它一般分为两类基本题型：一是已知轨迹类型求其方程，常用待定系数法，如求直线及圆的方程就是典型例题；二是未知轨迹类型，此时除了用代入法、交轨法、参数法等求轨迹的方法外，通常设法利用已知轨迹的定义解题，化归为求已知轨迹类型的轨迹方程。
因此在求动点轨迹方程的过程中，一是寻找与动点坐标有关的方程(等量关系)，侧重于数的运算，一是寻找与动点有关的几何条件，侧重于形，重视图形几何性质的运用。
求轨迹方程的一般步骤:建、设、现(限)、代、化.
　
　
　
　
　
　
　
　
　
　
　
轨迹方程
例31. 已知两点M(－2，0)，N(2，0)，点P满足=12，则点P的轨迹方程为(　　 )
　　　　　　　　　　　
例32.⊙O₁与⊙O₂的半径分别为1和2，|O₁O₂|=4，动圆与⊙O₁内切而与⊙O₂外切，则动圆圆心轨迹是(　 )
(A)椭圆　　　　　　　 (B)抛物线　　　　　　　　　 (C)双曲线　　　 (D)双曲线的一支
　
例33. 动点P在抛物线y²=-6x上运动,定点A(0,1),线段PA中点的轨迹方程是(　 )
(A)(2y+1)²=-12x(B)(2y+1)²=12x (C)(2y-1)²=-12x(D)(2y-1)²=12x
　
例34. 过点(2，0)与圆相内切的圆的圆心的轨迹是(　)
(A)椭圆　　(B)双曲线　　(C)抛物线　　(D)圆
　
例35. 已知的周长是16，，B则动点的轨迹方程是(　　 )
(A)(B) 　(C)　 (D)
　
例36. 椭圆中斜率为的平行弦中点的轨迹方程为　　　　.
　
例37. 已知动圆P与定圆C: (x+2)+y＝1相外切，又与定直线l：x＝1相切,那么动圆的圆心P的轨迹方程是______________.
　
例38. 在直角坐标系中,,则点的轨迹方程是______.
　
　
　
　
　
圆锥曲线综合问题
直线与圆锥曲线的位置关系
⑴直线与圆锥曲线的位置关系和判定
直线与圆锥曲线的位置关系有三种情况：相交、相切、相离.
直线方程是二元一次方程,圆锥曲线方程是二元二次方程,由它们组成的方程组,经过消元得到一个一元二次方程,直线和圆锥曲线相交、相切、相离的充分必要条件分别是、、.
⑵直线与圆锥曲线相交所得的弦长
直线具有斜率,直线与圆锥曲线的两个交点坐标分别为,则它的弦长
注:实质上是由两点间距离公式推导出来的,只是用了交点坐标设而不求的技巧而已(因为，运用韦达定理来进行计算.
当直线斜率不存在是,则.
注: 1.圆锥曲线，一要重视定义，这是学好圆锥曲线最重要的思想方法，二要数形结合，既熟练掌握方程组理论，又关注图形的几何性质，以简化运算。
2.当涉及到弦的中点时，通常有两种处理方法：一是韦达定理；二是点差法.
3.圆锥曲线中参数取值范围问题通常从两个途径思考:一是建立函数，用求值域的方法求范围；二是建立不等式，通过解不等式求范围。
　
　
　
　
圆锥曲线综合问题
例39. AB为过椭圆=1中心的弦，F(c，0)为椭圆的右焦点，则△AFB的面积最大值是(　　 )
(A)b² 　(B)ab　　　　　　　　　　　　　 (C)ac　　　　　　　　 (D)bc
例40. 若直线y＝kx+2与双曲线的右支交于不同的两点，则k的取值范围是(　)
,　,　　,　,
例41.若双曲线x²－y²=1右支上一点P(a, b)到直线y=x的距离为，则a+b的值是(　 ).
　　　　　　　　　　　或　　　(D)2或－2
　
　
　
　
　
　
　
　
　
　
圆锥曲线综合问题
例42.抛物线y=x²上的点到直线2x- y =4的距离最近的点的坐标是(　 )
)　　　　(B)(1,1)　　　　　　(C) ()　　　　　(D) (2,4)
例43. 抛物线y²=4x截直线所得弦长为3，则k的值是(　 )
(A)2　　　　　　(B)-2　　　　　　　(C)4　　　　　　　　(D)-4
例44. 把曲线按向量平移后得曲线，曲线有一条准线方程为，则的值为(　　 )
　　　　　　　　　　　　　　　　　　　
例45.如果直线与双曲线没有交点，则的取值范围是　　　 .
　
　
例46. 已知抛物线上两点关于直线对称，且，那么m的值为　　　 .
　
　
例47. 以双曲线－y²=1左焦点F，左准线l为相应焦点、准线的椭圆截直线y=kx+3所得弦恰被x轴平分，则k的取值范围是___________.
　
　
　
　
例48. 双曲线3x²-y²=1上是否存在关于直线y=2x对称的两点A、B?若存在，试求出A、B两点的坐标；若不存在，说明理由.
　
　
　
　
　
　
　

数学基础知识与典型例题(第八章圆锥曲线)答案

例1. D　　例2. B　例3. C　先考虑M+m=2a，然后用验证法.

例4. B提示：e=,P点到左准线的距离为2.5，它到左焦点的距离是2， 2a=10, P点到右焦点的距离是8，∴P点到右焦点的距离与到左焦点的距离之比是4 : 1;

例5. B∵，∴.

例6. C提示：椭圆3x²+4y²=48中，a=4, c=2, e=, 设椭圆上的P点到右准线的距离为d，则=, ∴|AP|+2|PF|=|AP|+d, ∴当AP平行于x轴且P点在A点与右准线之间时，|AP|+d为一直线段，距离最小，此时P点纵坐标等于，∴P点坐标是(2, )

例7. (3,4) 或(-3, 4)

例8. (1)或;　　　　 (2) ;

(3)或;　　　 (4) 或.

例9. ≤

例10. 解:设椭圆方程为+=1,(a>b>0)

⑴PQ⊥x轴时，F(-c,0)，|FP|=，又|FQ|=|FP|且OP⊥OQ，∴|OF|=|FP|,即c=∴ac=a²-c²,∴e²+e-1=0,∴e=与题设e=不符,所以PQ不垂直x轴.

⑵PQ∶y=k(x+c),P(x₁,y₁),Q(x₂,y₂),∵e=,∴a²=c²,b²=c²,

所以椭圆方程可化为:3x²+12y²-4c²=0,将PQ方程代入，

得(3+12k²)x²+24k²cx+12k²c²-4c²=0,∴x₁+x₂=,x₁x₂=

由|PQ|=得·=①

∵OP⊥OQ,∴·= -1即x₁x₂+y₁y₂=0,∴(1+k²)x₁x₂+k²c(x₁+x₂)+c²k²=0②

把，代入，解②得k²=，把代入①解得c²=3

∴a²=4,b²=1，则所求椭圆方程为+y²=1.

例11. B　　例12. C　　　例13. D　　　例14. C　　　　例15. C

例16. A假设,由双曲线定义且,

解得而由勾股定理得

[点评]考查双曲线定义和方程思想.

例17. 　　　　　　　　　例18.

例19.⑴设双曲线方程为(λ≠0),∴ ∴ ,

∴ 双曲线方程为;⑵设双曲线方程为∴ ,解之得k=4,∴ 双曲线方程为

评注：与双曲线共渐近线的双曲线方程为(λ≠0)，当λ>0时，焦点在x轴上；当λ<0时，焦点在y轴上。与双曲线共焦点的双曲线为(a²+k>0，b²-k>0)。比较上述两种解法可知，引入适当的参数可以提高解题质量，特别是充分利用含参数方程的几何意义，可以更准确地理解解析几何的基本思想.

例20. 解题思路分析：

法一：显然AB斜率存在设AB：y-2=k(x-1) 由得：(2-k²)x²-2k(2-k)x-k²+4k-6=0

当△>0时，设A(x₁,y₁)，B(x₂,y₂) 则∴ k=1，满足△>0∴ 直线AB：y=x+1

　法二：设A(x₁,y₁)，B(x₂,y₂)则两式相减得：(x₁-x₂)(x₁+x₂)=(y₁-y₂)(y₁+y₂)

　∵ x₁≠x₂∴ ∴ 　∴ AB：y=x+1代入得：△>0

评注：法一为韦达定理法，法二称为点差法，当涉及到弦的中点时，常用这两种途径处理。在利用点差法时，必须检验条件△>0是否成立。

(2)此类探索性命题通常肯定满足条件的结论存在，然后求出该结论，并检验是否满足所有条件.本题应着重分析圆的几何性质，以定圆心和定半径这两定为中心

设A、B、C、D共圆于⊙OM，因AB为弦，故M在AB垂直平分线即CD上；又CD为弦，故圆心M为CD中点。因此只需证CD中点M满足|MA|=|MB|=|MC|=|MD|

由得：A(-1，0)，B(3，4)又CD方程：y=-x+3

由得：x²+6x-11=0设C(x₃,y₃)，D(x₄,y₄)，CD中点M(x₀,y₀)

则∴ M(-3，6)

∴ |MC|=|MD|=|CD|=又|MA|=|MB|=∴ |MA|=|MB|=|MC|=|MD|

∴ A、B、C、D在以CD中点，M(-3，6)为圆心，为半径的圆上

评注：充分分析平面图形的几何性质可以使解题思路更清晰，在复习中必须引起足够重视.

例21. B()　　　　例22. B

例23. B(过P可作抛物线的切线两条，还有一条与x轴平行的直线也满足要求。)

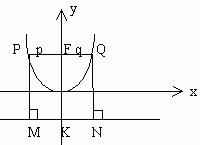例24. C作为选择题可采用特殊值法,取过焦点，且垂直于对称轴的直线与抛物线相交所形成线段分别为p,q，

则p=q=|FK|,

例25. 解析：运用抛物线的准线性质.答案：B　　例26. x²=8y　　例27. －p²

例28.　　例29.

例30. 解：由题意，直线AB不能是水平线，　故可设直线方程为：.

又设，则其坐标满足消去x得

由此得∴

因此,即.

故O必在圆H的圆周上.

又由题意圆心H()是AB的中点，

故由前已证

OH应是圆H的半径，

且.从而当k=0时，圆H的半径最小，亦使圆H的面积最小.此时，直线AB的方程为：x=2p.

注:1.解决直线和圆锥曲线的位置关系问题，一般方法是联立方程组，消元得一元二次方程，必须讨论二次项系数和判别式△，利用韦达定理寻找两根之和与两根之积之间的关系．求解有时借助图形的几何性质更为简洁．此题设直线方程为x=ky+2p；因为直线过x轴上是点Q(2p，0)，通常可以这样设，可避免对直线的斜率是否存在讨论．2．凡涉及弦的中点及中点弦问题，利用平方差法；涉及垂直关系往往也是利用韦达定理，设而不求简化运算．3．在引入点参数(本题中以AB弦的两个端点的坐标作为主参数)时，应尽量减少参数的个数，以便减少运算量．由OA⊥OB得x₁x₂+y₁y₂=O这个关系对于解决此类问题十分有用．4．列出目标函数，|OH|=P，运用函数思想解决解析几何中的最值问题是解决此类问题的基本思路，也可利用基本不等式a²+b²≥2ab当且仅当a=b时“=”成立求解．

例31. B　　　例32. D　　　　　例33. C　　　　例34. 　　　　A例35. B

例36. 9x+16y=0 (椭圆内部分　　　例37. y²＝－8x　例38.

例39. 解析：∵S_△_AFB=2S_△_AOF，∴当点A位于短轴顶点处面积最大.答案：D

例40. D41. B 42. B 数形结合估算出D

例43. D

例40. C∵由已知得曲线的准线为,∴焦点在轴上且,,

∴,∴

例45.k<　　　　例46.　　　　例47. (0，)

例48. 解：设AB：y=-x+m,代入双曲线方程得11x²+4mx-4(m²+1)=0,

这里△=(4m)²-4×11［-4(m²+1)］=16(2m²+11)＞0恒成立，

设A(x₁,y₁),B(x₂,y₂),AB的中点为M(x₀,y₀),则x₁+x₂=-，∴x₀=-,y₀=-x₀+m=,

若A、B关于直线y=2x对称，则M必在直线y=2x上，

∴=-得m=1，由双曲线的对称性知，直线y=-x与双曲线的交点的A、B必关于直线y=2x对称.

∴存在A、B且求得A(，-)，B(-，)

试题详情

2.双曲线的标准方程及其几何性质(如下表所示)

　
　
　
　
双曲线
例11.命题甲：动点P到两定点A、B的距离之差的绝对值等于2a(a>0)；命题乙：点P的轨迹是双曲线。则命题甲是命题乙的(　　　 )
(A) 充要条件　(B) 必要不充分条件　 (C) 充分不必要条件　(D) 不充分也不必要条件
　
例12.到定点的距离与到定直线的距离之比等于log₂3的点的轨迹是(　　 )
(A)圆　　　　　　　 (B)椭圆　　　　　　　　　 (C)双曲线　　　　　　　　　　　　 (D)抛物线
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
双曲线
例13. 过点(2，-2)且与双曲线有相同渐近线的双曲线的方程是(　　 )
(A)　　 (B)　　 (C)　 (D)
例14. 如果双曲线的焦距为6，两条准线间的距离为4，那么双曲线的离心率为( )
(A)　　　　 (B)　　　　(C)　　　　 (D)2
例15. 如果双曲线上一点到它的左焦点的距离是8，那么点到它的右准线的距离是(　)
(A)　　　　　　 (B)　　　　　 (C)　　　　　　　 (D)
例16. 双曲线的两焦点为在双曲线上,且满足,则的面积为(　　 )
　　　　　　　　　　　　　　　　　　　　　　　　
例17. 设的顶点，，且，则第三个顶点C的轨迹方程是________.
例18. 连结双曲线与(a＞0，b＞0)的四个顶点的四边形面积为，连结四个焦点的四边形的面积为，则的最大值是________．
例19.根据下列条件，求双曲线方程:
⑴与双曲线有共同渐近线，且过点(-3，)；
⑵与双曲线有公共焦点，且过点(，2).
例20. 设双曲线上两点A、B，AB中点M(1，2)
⑴求直线AB方程；
⑵如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D是否共圆，为什么？
　
　
　
抛物线知识关系网

　
　
　
　
　
　
　
　
抛物线
1.抛物线的定义:
平面内到定点F和定直线l的距离相等的点的轨迹叫做抛物线(点F不在上).定点F叫做抛物线的焦点, 定直线叫做抛物线的准线.
2.抛物线的标准方程及其几何性质(如下表所示)

标准方程
图形
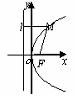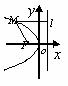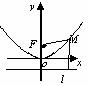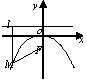对称轴	轴	轴	轴	轴
焦点
顶点	原点
准线
离心率	1
点P(x₀,y₀) 的焦半径公式	用到焦半径自己推导一下即可如:开口向右的抛物线上的点P(x₀,y₀)的焦半径等于x₀+.

注: 1.通径为2p，这是抛物线的过焦点的所有弦中最短的弦.

试题详情

⑴平面向量基本定理:如果是同一平面内两个不共线的向量,那么对于这个平面内任一向量,有且只有一对实数,使，称为的线性组合。

①其中叫做表示这一平面内所有向量的基底;

②平面内任一向量都可以沿两个不共线向量的方向分解为两个向量的和,并且这种分解是唯一的.

这说明如果且,那么.

③当基底是两个互相垂直的单位向量时,就建立了平面直角坐标系,因此平面向量基本定理实际上是平面向量坐标表示的基础.

　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
向量的
概念及运算
向量坐标与点坐标的关系：当向量起点在原点时，定义向量坐标为终点坐标，
即若A(x，y)，则=(x,y)；当向量起点不在原点时，向量坐标为终点坐标减去起点坐标，即若A(x₁,y₁)，B(x₂,y₂)，则=(x₂-x₁,y₂-y₁)
⑵两个向量平行的充要条件
符号语言：
坐标语言为：设非零向量,则∥(x₁,y₁)=λ(x₂,y₂)，
即,或x₁y₂-x₂y₁=0, 在这里,实数λ是唯一存在的,当与同向时,λ>0；当与异向时,λ<0。|λ|=,λ的大小由及的大小确定。因此,当,确定时，λ的符号与大小就确定了.这就是实数乘向量中λ的几何意义。
⑶两个向量垂直的充要条件
符号语言：
坐标语言：设非零向量，则

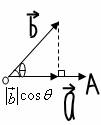⑷两个向量数量积的重要性质：
① 即 (求线段的长度);
②(垂直的判断);
③ (求角度)。
以上结论可以(从向量角度)有效地分析有关垂直、长度、角度等问题,由此可以看到向量知识的重要价值.
注:①两向量,的数量积运算结果是一个数(其中),这个数的大小与两个向量的长度及其夹角的余弦有关.
　 ②叫做向量在方向上的投影(如图).
数量积的几何意义是数量积等于的模与在方向上的投影的积.
③如果,,则=,
∴,这就是平面内两点间的距离公式.
向量的
概念及运算
例1．在中，(　 )
　　　　　　　　　　　　
例2.平面内三点,若∥，则x的值为(　)
(A)-5　　　　　(B)-1 　　　　　(C)1　　　　　(D)5
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
　
向量的
概念及运算
例3. 设，，是任意的非零平面向量，且相互不共线，则：
①(·)(·)=0　　　　　　　　 ②||-||<||
③(·)(·)不与垂直　 ④(3+2)·(32)=9||²- 4|²中，
真命题是(　 )(A)①②　　 (B)②③　　 (C)③④　　　 (D)②④
例4. △OAB中,=,=,=,若=，t∈R，则点P在(　 )
(A)∠AOB平分线所在直线上　　　(B)线段AB中垂线上
(C)AB边所在直线上　　　　　　(D)AB边的中线上
例5. 正方形对角线交点为M，坐标原点O不在正方形内部，且=(0，3)，=(4，0)，则=(　 )
(A)() 　(B)()　　 (C)(7，4)　 (D)()
例6.已知,则实数x=_______.
例7.已知则_____, ______,与的夹角的余弦值是_____.
例8. 已知的三个顶点分别为求的大小.
　
　
　
　
例9. 已知△ABC中，A(2，-1)，B(3，2)，C(-3，-1)，BC边上的高为AD，求点D和向量坐标。
　
　
　
　
　
　
例10.在△OAB的边OA、OB上分别取点M、N，使||∶||=1∶3，||∶||=1∶4，设线段AN与BM交于点P，记= ，=，用，表示向量.
　
　
　
　
　
　
　
　
　
　
定比分点
线段的定比分点
1.定义:设是直线上的两点,点P是上不同于的任意一点,则存在一个实数使,叫做点P分有向线段所成的比.(如图)

　
①P在线段上,P为内分点时,;
②P在线段或的延长线上, P为外分点时,.
③内分取 “+”, 外分取 “一”.
2. 定比分点坐标公式:
设、、，
则： ,
特殊地，得中点坐标公式：
另外，注意一下定比分点的向量公式：
　 O为平面内任意一点，
则.
　有时直接运用它来考虑更简便!
3. 三角形重心公式及推导(见课本例2)：
三角形重心公式：
例11.点A(m,n)关于点B(a,b)对称点的坐标是( )
(A)(－m，－n)　
(B)(a－m，b－n)
(C)(a－2m，b－2n)
(D)(2a－m，2b－n)
例12．设，直线AB交轴于C点，则点C分所成的比为()
　　　
　　
平移
1.图形平移：设F是坐标平面内的一个图形，将F上所有的点按照同一方向移动同样长度(即按向量平移)，得到图形F`，我们把这一过程叫做图形的平移。
2.平移公式：点按
向量平移到
则(新=旧+移)
其中叫做平移向量.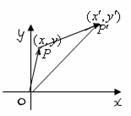

3. ⑴设曲线C：y=f(x)按=(h，k)平移，则平移后曲线对应的解析式为,当h，k中有一个为零时，就是前面已经研究过的左右及上下平移.
注:函数图象平移口诀:左加右减,上加下减.　注意这里是指函数解析式的变化,另外注意顺序性.
例13.设向量,则将按平移得到的坐标表示为(　 )
(A)(0,1)　　　 (B)(4,-11)　
(C)(7,-5)　　 (D)(3,6)
例14.若将曲线C₁:平移到C₂,使得曲线C₁上一点P的坐标由(1,0)变为(2,2),则C₂的方程是( )
(A)(B)
(C)(D)
例15. 把函数的图象按平移后得到的函数解析式为____.
解三角形
解斜三角形：
常用的主要结论有：
(1)A+B+C=180⁰　　　⑵任意两边之和大于第三边,任意两边之差小于第三边.
⑶等边对等角:;　大边对大角:.
⑷底×高=(其中是内切圆半径)

⑸(正弦定理)
　
⑹(余弦定理)
　
解三角形
例16.在中,,则a等于(　 )
(A) 　　　(B)　　　　　 (C) 　　　(D)
例17.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30⁰,60⁰,则塔高为(　 )
(A)米　　　(B)米　　　　(C)米　　(D)米
例18．在中，，,若这个三角形有两解，则的取值范围是(　 )
　　　　　　　　　　

数学基础知识与典型例题(第5章平面向量)答案

例1A、例2.C、例3.D、例4.A、例5.A、例6.6、例7.,,、例8.