
5. 3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在,画
出这个算法的流程图.
4. 在表示求直线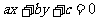 (
(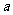 ,
,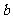 为常数,且
为常数,且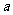 ,
,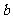 不同时为0)的斜率的算法
不同时为0)的斜率的算法
的流程图中,判断框中应填入的内容是
3.将“打电话”的过程描述成一个算法,这个算法可表示为 ,由此说明算法具有下列特性 .
1.
下面流程图中的错误是( )


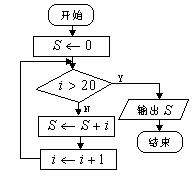


图13-1-11

A.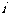 没有赋值 B.循环结构有错
没有赋值 B.循环结构有错 

C.S的计算不对 D.判断条件不成立

1.已知两个单元分别存放了变量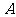 和
和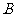 的值,则可以实现变量
的值,则可以实现变量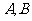 交换的算法是( ).
交换的算法是( ).

A.S1  B.S1
B.S1  C.S1
C.S1  D.S1
D.S1 


S2 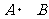 S2
S2  S2
S2 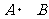 S2
S2



S3  S3
S3 


[例1] 已知三个单元存放了变量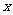 ,
,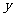 ,
,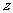 的值,试给出一个算法,顺次交换
的值,试给出一个算法,顺次交换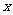 ,
,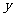 ,
,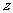 的值(即
的值(即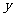 取
取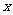 的值,
的值,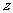 取
取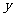 的值,
的值,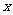 取
取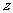 的值),并画出流程图.
的值),并画出流程图.

错解:第一步 


第二步 


第三步 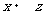


流程图为 

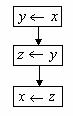


图13-1-3 

错因:未理解赋值的含义,由上面的算法使得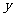 ,
,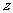 均取
均取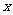 的值.
的值.

举一形象的例子:有蓝和黑两个墨水瓶,但现在却把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.对于这种非数值性问题的算法设计问题,应当首先建立过程模型,根据过程设计步骤完成算法. 我们不可将两个墨水瓶中的墨水直接交换,因为两个墨水瓶都装有墨水,不可能进行直接交换.正确的解法应为:

S1 取一只空的墨水瓶,设其为白色;

S2
将黑墨水瓶中的蓝墨水装入白瓶中;

S3 将蓝墨水瓶中的黑墨水装入黑瓶中;

S4 将白瓶中的蓝墨水装入蓝瓶中;

S5 交换结束.

正解:第一步 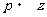 {先将
{先将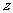 的值赋给变量
的值赋给变量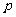 ,这时存放
,这时存放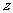 的单元可作它用}
的单元可作它用} 

第二步  {再将
{再将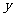 的值赋给
的值赋给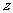 ,这时存放
,这时存放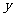 的单元可作它用}
的单元可作它用} 

第三步  {同样将
{同样将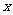 的值赋给
的值赋给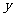 ,这时存放
,这时存放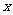 的单元可作它用}
的单元可作它用} 

第四步  {最后将
{最后将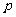 的值赋给
的值赋给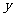 ,三个变量
,三个变量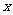 ,
,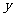 ,
,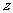 的值就完成了交换}
的值就完成了交换}

流程图为

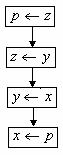


图13-1-4

点评:在计算机中,每个变量都分配了一个存储单元,为了达到交换的目的,需要一个单元存放中间变量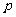 .
.

[例2]已知三个数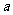 ,
,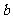 ,
, .试给出寻找这三个数中最大的一个算法,画出该算法的流程图.
.试给出寻找这三个数中最大的一个算法,画出该算法的流程图.

解:流程图为

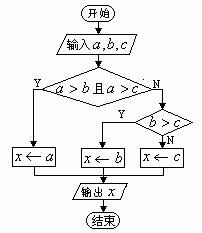












图13-1-5

点评:条件结构可含有多个判断框,判断框内的内容要简明、准确、清晰.此题也可将第一个判断框中的两个条件分别用两个判断框表示,两两比较也很清晰.若改为求100个数中的最大数或最小数的问题则选择此法较繁琐,可采用假设第一数最大(最小)将第一个数与后面的数依依比较,若后面的数较大(较小),则进行交换,最终第一个数即为最大(最小)值.

点评:求和时根据过程的类同性可用循环结构来实现,而不用顺序结构.

[例3]画出求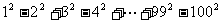 的值的算法流程图.
的值的算法流程图.

解:这是一个求和问题,可采用循环结构实现设计算法,但要注意奇数项为正号,偶数项为负号.

思路一:采用-1的奇偶次方(利用循环变量)来解决正负符号问题;

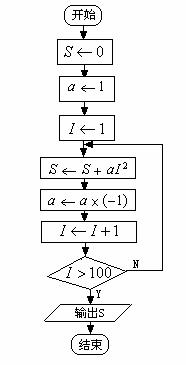
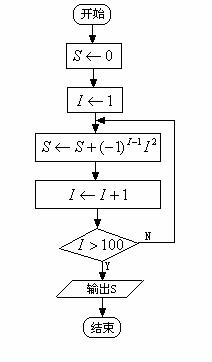


图13-1-6
图13-1-7

思路二:采用选择结构分奇偶项求和;

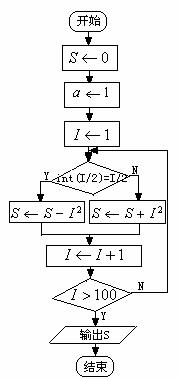


图13-1-8

思路三:可先将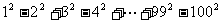 化简成
化简成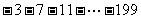 ,转化为一个等差数列求和问题,易利用循环结构求出结果.
,转化为一个等差数列求和问题,易利用循环结构求出结果.


[例4] 设计一算法,求使 成立的最小正整数
成立的最小正整数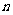 的值.
的值.

解: 流程图为 

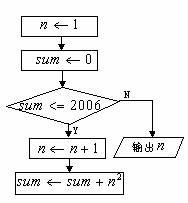


图13-1-9

点评:这道题仍然是考察求和的循环结构的运用问题,需要强调的是求和语句的表示方法.若将题改为求使 成立的最大正整数
成立的最大正整数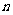 的值时,则需注意的是输出的值.
的值时,则需注意的是输出的值.

[例5]任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判断.

解:算法为:

S1
判断n是否等于2,若n=2,则n是质数;若n>2 ,则执行S2
,则执行S2

S2
依次从2-n-1检验是不是的因数,即整除n的数,若有这样的数,则n不是质数;若没有这样的数,则n是质数.

点评:要验证是否为质数首先必须对质数的本质含义作深入分析:

(1)质数是只能被1和自身整除的大于1的整数.

(2)要判断一个大于1的整数n是否为质数,只要根据定义,用比这个整数小的数去除n.如果它只能被1和本身整除,而不能被其它整数整除,则这个数便是质数.

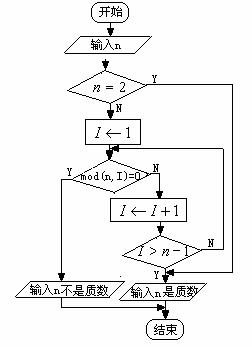


图13-1-10


[例6]设计一个求无理数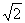 的近似值的算法.
的近似值的算法.

分析:无理数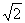 的近似值可看作是方程
的近似值可看作是方程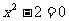 的正的近似根,因此该算法的实质是设计一个求方程
的正的近似根,因此该算法的实质是设计一个求方程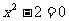 的近似根的算法.其基本方法即运用二分法求解方程的近似解.
的近似根的算法.其基本方法即运用二分法求解方程的近似解.

解:设所求近似根与精确解的差的绝对值不超过0.005,算法:

S1 令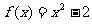 .因为
.因为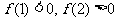 ,所以设
,所以设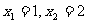


S2 令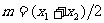 ,判断
,判断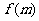 是否为0,若是,则m为所求;若否,则继续判断
是否为0,若是,则m为所求;若否,则继续判断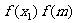 大于0还是小于0.
大于0还是小于0.


S3 若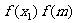 >0,则
>0,则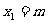 ;否则,令
;否则,令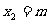 .
.

S4 判断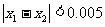 是否成立,若是,则
是否成立,若是,则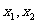 之间的任意值均为满足条件的近似根;若否,则返回第二步.
之间的任意值均为满足条件的近似根;若否,则返回第二步.

点评:二分法求方程近似解的算法是一个重要的算法案例,将在第三节中详细阐述.

3. 算法三种逻辑结构的几点说明:

(1)顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的.在流程图中的体现就是用流程线自上而下地连接起来,按顺序执行算法步骤.(2)一个条件结构可以有多个判断框.

(3)循环结构要在某个条件下终止循环,这就需要条件结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用语输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次.

2. 画流程图时必须注意以下几方面:

(1)使用标准的图形符号.

(2)流程图一般按从上到下、从左到右的方向画.

(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框具有超过一个退出点的唯一符号.

(4)判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.

(5)在图形符号内描述的语言要非常简练清楚.

1.“算法“没有一个精确化的定义,教科书只对它作了描述性说明,算法具有如下特点:

(1)有限性:一个算法的步骤是有限的,必须在有限操作之后停止,不能是无限的.

(2)确定性:算法的每一步骤和次序应当是确定的.

(3)有效性:算法的每一步骤都必须是有效的.

3.根据对条件的不同处理,循环结构又分为两种:

直到型(until型)循环:在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时执行循环体.满足则停止.如图13-1-3,先执行A框,再判断给定的条件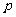 是否为“假”,若
是否为“假”,若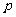 为“假”,则再执行A,如此反复,直到
为“假”,则再执行A,如此反复,直到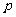 为“真”为止.
为“真”为止. 

当型(while型)循环:在每次执行循环体前对控制循环条件进行判断,当条件满足时执行循环体,不满足则停止.如图13-1-4,当给定的条件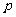 成立(“真”)时,反复执行A框操作,直到条件
成立(“真”)时,反复执行A框操作,直到条件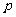 为“假”时才停止循环.
为“假”时才停止循环.

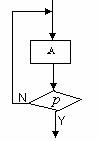
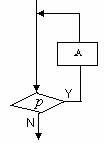


图13-1-1
图13-1-2

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com