
6.物块A、B放在光滑水平面上并用轻质弹簧做成的弹簧秤相连,如图所示.今对物体A、B分别施以方向相反的水平力F1、F2.且F1小于F2,则弹簧秤的示数( C )
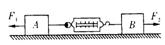
A.一定等于F1+F2 B.一定等于F1-F2
C.一定大于F1小于F2 D.条件不足,无法确定
5.如图所示,在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A,A与竖直墙之间放一光滑圆球B,整个装置处于静止状态。现对B加一竖直向下的力F,F的作用线通过球心,设墙对B的作用力为F1,B对A的作用力为F2,地面对A的支持力为F3,地面对A的摩擦力为F4.若F缓慢增大而整个装置仍保持静止,则在此过程中( C )
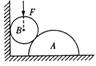
A.F1保持不变,F3缓慢增大 B.F1缓慢增大,F3保持不变
C.F2缓慢增大,F4缓慢增大 D.F2缓慢增大,F4保持不变
4.如图所示,在斜面上有两个物体A、B靠在一起往下滑,对于A的受力情况,下列说法正确的是( BCD )
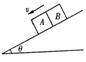
A.若斜面光滑,并设物体A、B的质量分别为mA、mB,且mB>mA,则物体A受三个力
B.若斜面光滑,则物体A只受两个力
C.若物体A、B与斜面间有摩擦且动摩擦因数相同,则物体A只受三个力
D.若物体A、B与斜面间有摩擦,则A可能受四个力
3.甲、乙两球队位于同一竖直直线上的不同高度,甲比乙高,将甲、乙两球分别发大小为v1和v2的初速度沿同一水平方向抛出,不计空气阻力,下列情况中有可能使两球相遇的是( D )
A.同时抛出,且v1<v2 B. 甲迟抛出,且v1<v2
C.甲早抛出,且v1>v2 D.甲早抛出,且v1<v2
2.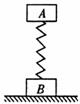 如图所示,质量均为m的物体A和B通过一劲度系数为k的轻弹簧相连,B放在地面上,开始时AB都处于静止状态。若通过细绳缓慢地将A向上提升,B刚要离开地面时,A上升的距离为L1;若通过细绳将A加速向提升,B刚要离要时,A上升的距离的L2. 假设弹簧一直在弹性限度内,则( B )
如图所示,质量均为m的物体A和B通过一劲度系数为k的轻弹簧相连,B放在地面上,开始时AB都处于静止状态。若通过细绳缓慢地将A向上提升,B刚要离开地面时,A上升的距离为L1;若通过细绳将A加速向提升,B刚要离要时,A上升的距离的L2. 假设弹簧一直在弹性限度内,则( B )
A. L1=L2=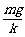 B. L1=L2=
B. L1=L2=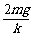
C. L1=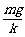 , L2<L1
D. L1=
, L2<L1
D. L1=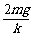 ,L2<L1
,L2<L1
1.下列关于超重、失重现象的描述中,正确的是( BD )
A.电梯正在上升,人在电梯中一定处于超重状态
B.在国际空间站内的宇航员处于完全失重状态
C.列车在水平轨道上加速行驶,车上的人处于超重状态
D.荡秋千时当秋千摆到最低位置时,人处于超重状态
(四)机械能守恒定律:
内容:_______________________________________________________
________________________________________________;
条件:只有重力(弹力)做功,其他力不做功。这里的弹力指研究弹性势能的物体(如弹簧)的弹力,不是指通常的拉力、推力。不能误认为“只受重力(弹力)作用。
表达式:E2=E1。
注意:(1)研究对象是系统;(2)分清初、末状态。
推导:应用等量转换法,根据动能定理 WG=EK2-EK1
推出 EK2+ EP2= EK1+ EP1
重力做功与重力势能的关系 WG=EP1-EP2 (即E1=E2)
课堂小结:
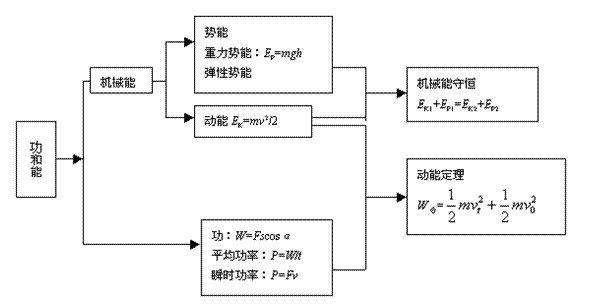 本章的知识结构图:
本章的知识结构图:
课外作业:
1.整理本章所学知识。
(三)重力势能和弹性势能:
1.重力势能:
(1)重力做功的特点:重力对物体做的功只跟起点和终点的位置有关,而跟物体的运动的路径无关。即重力是保守力,因而可以引入势能的概念。
(2)重力势能的定义:
文字表述:_____________________________________________;
公式表示:
性质:重力势能是标量、状态量、相对量。当物体位于所选择的参考平面(零势面)的上方(下方)时,重力势能为正直(负值)。但重力势能的差值与参考平面的选择无关。重力势能属于物体和地球组成的系统。
(3)重力势能与重力做功的联系:重力做的功等于物体的重力势能的减小,即WG=mgh1-mgh2;如重力做负功,即mgh1<mgh2,重力势能增加。
2.弹性势能:
定义:文字表述:______________________________________________;
性质:弹性势能是标量、状态量。
注意:弹性势能EP的大小与弹簧的伸长量或者压缩量x的大小有关,对于同一根弹簧,弹簧的伸长量或者压缩量x越大,弹性势能EP越大。
弹性势能与弹力做的功的联系:弹力做的功等于弹簧的弹性势能的减小。
(二)动能和动能定理:
1.动能:
定义:文字表述:________________________________________________;
公式表示:___________________。
性质:动能是标量。注意:动能没有方向,不要把速度的方向误认为是动能的方向。 动能是状态量、动能是相对量,同一物体相对于不同参照物其动能可能不同。动能与动量不同,动量是矢量,动量变化而动能不一定变化。例如匀速圆周运动,动量在不断改变,而动能不改变。动量的大小和动能关系为:P2=2mEk.
2.动能定理:
文字表述:____________________________________________________;
公式表示: W=EK2-EK1 ;
讨论:当W>0时, EK2 > EK1 ,动能增大;当W<0时, EK2 < EK1 动能减小;当W=0时 EK2 = EK1 动能不变。
注意:(1)功和能是两个不同的概念,但相互之间有密切的联系,这种联系体现于动能定理上,外力对物体做的总功等于物体动能的增加,一般来说,不是等于物体动能的本身。
(2)外力对物体所做的总功等于物体受到的所有外力的功(包括各段的运动过程)的代数和。
(3)适用对象:适用于单个物体。
(一)功和功率:
1.功:
功的计算公式: 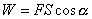
做功的两个不可缺少的因素:(1)力;(2)在力的方向上发生的位移;功是标量、是过程量。
注意:当 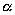 =
= 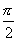 时,W=0。例如:线吊小球做圆周运动时,线的拉力不做功;洛仑磁力不做功。当
时,W=0。例如:线吊小球做圆周运动时,线的拉力不做功;洛仑磁力不做功。当
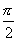 <
< 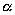
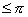 时,力对物体做负功,也说成物体克服这个力做了功(取正值)
时,力对物体做负功,也说成物体克服这个力做了功(取正值)
2.功率:
定义:文字表述:_________________________________________________;
公式表示:_________________;
物理意义:___________________________;
国际单位:__________;其他单位:1千瓦=1000瓦特、1马力=0.735千瓦。
其他计算公式:平均功率_____________________;
瞬时功率_____________________。
额定功率是发动机正常工作时的最大功率;实际输出功率小于或等于额定功率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com