1.集合M＝{x|x＝sin，n∈Z}，N＝{x|x＝cos，n∈N}，则M∩N等于　　　　 (　)

A.{－1,0,1}　　B.{0,1}　　　　　 C.{0} 　　　　　　　D.∅

解析：∵M＝{x|x＝sin，n∈Z}＝{－，0，}，

N＝{－1,0,1}，

∴M∩N＝{0}.

答案：C

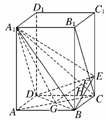
21. (本小题满分14分)(2009·泰州模拟)如图，E、F分别为直角三角形ABC的直角边AC和斜边AB的中点，沿EF将△AEF折起到△A′EF的位置，连结A′B、A′C，P为A′C的中点.

(1)求证：EP∥平面A′FB；

(2)求证：平面A′EC⊥平面A′BC；

(3)求证：AA′⊥平面A′BC.

证明：(1)∵E、P分别为AC、A′C的中点，

∴EP∥A′A，又A′A⊂平面AA′B，EP⊄平面AA′B，

∴EP∥平面AA′B，

即EP∥平面A′FB.

(2)∵BC⊥AC，由题意知EF⊥A′E，EF∥BC，

∴BC⊥A′E，又∵A′E∩AC＝E，

∴BC⊥平面A′EC，BC⊂平面A′BC，

∴平面A′BC⊥平面A′EC.

(3)在△A′EC中，P为A′C的中点，

又A′E＝EC，∴EP⊥A′C，

在△A′AC中，EP∥A′A，∴A′A⊥A′C.

由(2)知：BC⊥平面A′EC，又A′A⊂平面A′EC，

∴BC⊥AA′，∵BC∩A′C＝C，∴A′A⊥平面A′BC.

20.(本小题满分13分)已知ABCD是矩形，AD＝4，AB＝2，E、F分别是线段AB、BC的中点，PA⊥平面ABCD.

(1)证明：PF⊥FD；

(2)在PA上找一点G，使得EG∥平面PFD.

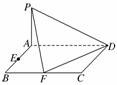
解：(1)证明：连接AF，则AF＝2，DF＝2，

又AD＝4，∴DF²+AF²＝AD²，

∴DF⊥AF.又PA⊥平面ABCD，

∴DF⊥PA，又PA∩AF＝A，

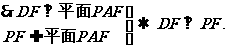
(2)过点E作EH∥FD交AD于点H，则EH∥平面PFD且AH＝AD.

再过点H作HG∥DP交PA于点G，则HG∥平面PFD且AG＝AP，

∴平面EHG∥平面PFD.

∴EG∥平面PFD.

从而满足AG＝AP的点G为所求.

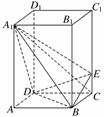
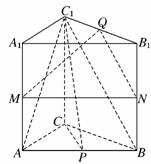
19. (本小题满分12分)(2009·南通模拟)如图，已知在三棱柱ABC－A₁B₁C₁中，AA₁⊥平面ABC，AC＝BC，M、N、P、Q分别是AA₁、BB₁、AB、B₁C₁的中点.

(1)求证：平面PCC₁⊥平面MNQ；

(2)求证：PC₁∥平面MNQ.

证明：(1)∵AC＝BC，P为AB的中点，∴AB⊥PC，

又CC₁∥AA₁，

AA₁⊥平面ABC，

∴CC₁⊥平面ABC，

∴CC₁⊥AB，

又∵CC₁∩PC＝C，

∴AB⊥平面PCC₁，

由题意知MN∥AB，故MN⊥平面PCC₁，

MN在平面MNQ内，

∴平面PCC₁⊥平面MNQ.

(2)连接AC₁、BC₁，∵BC₁∥NQ，AB∥MN，

又BC₁∩AB＝B，

∴平面ABC₁∥平面MNQ，

∵PC₁在平面ABC₁内，

∴PC₁∥平面MNQ.

18.(本小题满分12分)(2010·徐州模拟)如图，PA垂直于矩形ABCD所在的平面，AD＝PA＝2，CD＝2，E、F分别是AB、PD的中点.

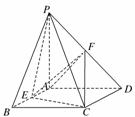
(1)求证：AF∥平面PCE；

(2)求证：平面PCE⊥平面PCD；

(3)求四面体PEFC的体积.

解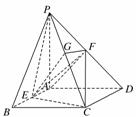：(1)证明：设G为PC的中点，连结FG，EG，

∵F为PD的中点，E为AB的中点，

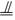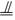∴FG CD，AECD

∴FG 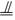　AE，∴AF∥GE

∵GE⊂平面PEC，

∴AF∥平面PCE；

(2)证明：∵PA＝AD＝2，∴AF⊥PD

又∵PA⊥平面ABCD，CD⊂平面ABCD，

∴PA⊥CD，∵AD⊥CD，PA∩AD＝A，

∴CD⊥平面PAD，

∵AF⊂平面PAD，∴AF⊥CD.

∵PD∩CD＝D，∴AF⊥平面PCD，

∴GE⊥平面PCD，

∵GE⊂平面PEC，

∴平面PCE⊥平面PCD；

(3)由(2)知，GE⊥平面PCD，

所以EG为四面体PEFC的高，

又GF∥CD，所以GF⊥PD，

EG＝AF＝，GF＝CD＝，

S_△PCF＝PD·GF＝2.

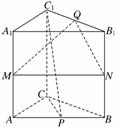得四面体PEFC的体积V＝S_△PCF·EG＝.

17.(本小题满分12分)已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1+，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使DE⊥EC.

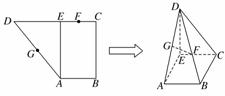
(1)求证：BC⊥平面CDE；

(2)求证：FG∥平面BCD；

(3)求四棱锥D－ABCE的体积.

解：(1)证明：由已知得：

DE⊥AE，DE⊥EC，∴DE⊥平面ABCE.

∴DE⊥BC.又BC⊥CE，CE∩DE＝E，

∴BC⊥平面DCE.

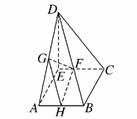
(2)证明：取AB中点H，连结GH，FH，

∴GH∥BD，FH∥BC，

∴GH∥平面BCD，FH∥平面BCD.

又GH∩FH＝H，

∴平面FHG∥平面BCD，

∴FG∥平面BCD(由线线平行证明亦可).

(3)V＝×1×2×＝.

骤)

16．(本小题满分12分)(2010·泉州模拟)如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形，尺寸如图所示)．

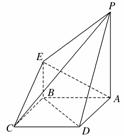
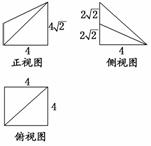
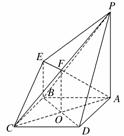
(1)求四棱锥P-ABCD的体积；

(2)证明：BD∥平面PEC；

(3)若G为BC上的动点，求证：AE⊥PG.

解：(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4，BE＝2，AB＝AD＝CD＝CB＝4，

∴V_P－ABCD＝PA×S_ABCD＝×4×4×4＝.

(2)证明：连结AC交BD于O点，

取PC中点F，连结OF，

∵EB∥PA，且EB＝PA，

又OF∥PA，且OF＝PA，

∴EB∥OF，且EB＝OF，

∴四边形EBOF为平行四边形，

∴EF∥BD.

又EF⊂平面PEC，BD⊄平面PEC，所以BD∥平面PEC.

(3)连结BP，∵＝＝，∠EBA＝∠BAP＝90°，

∴△EBA∽△BAP，∴∠PBA＝∠BEA，

∴∠PBA+∠BAE＝∠BEA+∠BAE＝90°，

∴PB⊥AE.

又∵BC⊥平面APEB，∴BC⊥AE，

∴AE⊥平面PBG，∴AE⊥PG.

15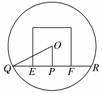．(2009·江南测试)棱长为a的正方体ABCD－A₁B₁C₁D₁的8个顶点都在球O的表面上，E、F分别是棱AA₁、DD₁的中点，则直线EF被球O截得的线段长为________．

解析：因为正方体内接于球，所以2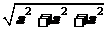R=，R=，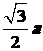

过球心O和点E、F的大圆的截面图如图所示，

则直线被球截得的线段为QR，过点O作OP⊥QR

于点P，所以，在△QPO中，QR=2QP=2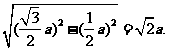

答案：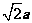

14．母线长为1的圆锥的侧面展开图的圆心角等于π，则该圆锥的体积为________．

解析：圆锥的侧面展开图扇形的弧长，即底面圆的周长为π·1＝π，于是设底面圆的半径为r，

则有2πr＝π，所以r＝，

于是圆锥的高为h＝＝，

故圆锥的体积为V＝π.

答案：π

13.如图，正方体ABCD-A₁B₁C₁D₁中，M∈A₁B，

N∈B₁C，A1M=B₁N，有以下四个结论：

①A₁A⊥MN；

②AC∥MN；

③MN与平面ABCD成0°角；

④MN与AC是异面直线．

其中正确结论的序号是　　　.

解析：易知①③④正确．

答案：①③④