19.(本小题满分12分)某公司生产一种产品的固定成本为0.5万元，但每生产100件需再增加 成本0.25万元，市场对此产品的年需求量为500件，年销售收入(单位：万元)为R(t)＝5t－(0≤t≤5)，其中t为产品售出的数量(单位：百件).

(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x)；

(2)当年产量为多少件时，公司可获得最大年利润？

解：(1)当0≤x≤5时，f(x)＝R(x)－0.5－0.25x

＝－x²+4.75x－0.5；当x>5时，

f(x)＝R(5)－0.5－0.25x＝12－0.25x，

故所求函数解析式为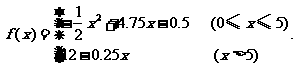

(2)0≤x≤5时，f(x)＝－(x－4.75)²+10.78125，

∴在x＝4.75时，

f(x)有最大值10.78125，当x>5时，

f(x)＝12－0.25x<12－0.25×5

＝10.75<10.78125，

综上所述，当x＝4.75时，f(x)有最大值，即当年产量为475件时，公司可获得最大年利润.

18.(本小题满分12分)已知函数f(x)＝ax+(x≠0，常数a∈R).

(1)讨论函数f(x)的奇偶性，并说明理由；

(2)若函数f(x)在x∈[3，+∞)上为增函数，求a的取值范围.

解：(1)定义域(－∞，0)∪(0，+∞)，关于原点对称.

当a＝0时，f(x)＝，满足对定义域上任意x，f(－x)＝f(x)，∴a＝0时，f(x)是偶函数；

当a≠0时，f(1)＝a+1，f(－1)＝1－a，

若f(x)为偶函数，则a+1＝1－a，a＝0矛盾；

若f(x)为奇函数，

则1－a＝－(a+1),1＝－1矛盾，∴当a≠0时，f(x)是非奇非偶函数.

(2)任取x₁>x₂≥3，f(x₁)－f(x₂)＝ax₁+－ax₂－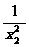

＝a(x₁－x₂)+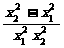＝(x₁－x₂)(a－).

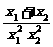∵x₁－x₂>0，f(x)在[3，+∞)上为增函数，

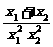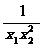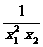∴a>，即a>+在[3，+∞)上恒成立.

∵+<，

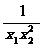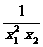∴a≥.

17.(本小题满分12分)已知函数f(x)＝x⁴－4x³+ax²－1在区间[0,1]上单调递增，在区间[1,2]上单调递减.

(1)求a的值；

(2)记g(x)＝bx²－1，若方程f(x)＝g(x)的解集恰有3个元素，求b的取值范围.

解：(1)f′(x)＝4x³－12x²+2ax，因为f(x)在[0,1]上递增，在[1,2]上递减，所以x＝1是f(x)的极值点，所以f′(1)＝0，

即4×1³－12×1²+2a×1＝0.

解得a＝4，经检验满足题意，所以a＝4.

(2)由f(x)＝g(x)可得

x²(x²－4x+4－b)＝0，

由题意知此方程有三个不相等的实数根，

此时x＝0为方程的一实数根，则方程x²－4x+4－b＝0应有两个不相等的非零实根，

所以Δ>0，且4－b≠0，

即(－4)²－4(4－b)>0且b≠4，

解得b>0且b≠4，

所以所求b的取值范围是(0,4)∪(4，+∞).

16.(本小题满分12分)已知函数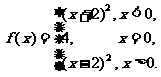

(1)写出f(x)的单调区间；

(2)若f(x)＝16，求相应x的值.

解：(1)f(x)的单调增区间为[－2,0)，(2，+∞)，

单调减区间为(－∞，－2)，(0,2].

(2)由f(x)＝16

∴(x+2)²＝16，∴x＝2(舍)或－6；

或(x－2)²＝16，∴x＝6或－2(舍).

∴x的值为6或－6.

15.已知函数f(x)＝x²－cosx，对于上的任意x₁，x₂，有如下条件：

①x₁>x₂；②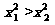；③|x₁|>x₂.

其中能使f(x₁)>f(x₂)恒成立的条件序号是　　.

解析：函数f(x)为偶函数，f′(x)＝2x+sinx，

当0＜x≤时，0<sinx≤1,0<2x≤π，

∴f′(x)>0，函数f(x)在上为单调增函数，

由偶函数性质知函数在上为减函数.

当x>x时，得|x₁|>|x₂|≥0，

∴f(|x₁|)>f(|x₂|)，由函数f(x)在上为偶函数得f(x₁)>f(x₂)，故②成立.

∵>－，而f ＝f ，

∴①不成立，同理可知③不成立.故答案是②.

答案：②

14.已知函数f(x)＝log₂(x²－ax+3a)，对于任意x≥2，当Δx>0时，恒有f(x+Δx)>f(x)，则实数a的取值范围是　　.

解析：依题意，对于任意x≥2，当Δx>0时，恒有f(x+Δx)>f(x)，说明函数f(x)在[2，+∞)上是单调递增函数，所以应有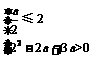，解得－4<a≤4，此即为实数a的取值范围.

答案：(－4,4]

13.设函数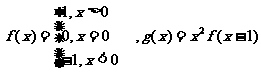 函数g(x)的递减区间是　　.

解析：依题意有g(x)=x² f(x-1)=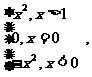

所以g(x)的递减区间是(0,1).

答案：(0,1)

12.函数y＝log₃(9－x²)的定义域为A，值域为B，则A∩B＝　　.

解析：由9－x²>0⇒－3<x<3，

则A＝(－3,3).又0<9－x²≤9，

∴y＝log₃(9－x²)≤2，则B＝(－∞，2].

所以A∩B＝(－3,2].

答案：(－3,2]

11．(2010·福州模拟)关于x的方程(m+3)x²－4mx+2m－1＝0的两根异号，且负数根的绝对值比正数根大，那么实数m的取值范围是________．

解析：∵x₁x₂<0，x₁+x₂<0，

∴，解得－3<m<0.

答案：(－3,0)

10.定义在R上的函数f(x)，如果存在函数g(x)＝kx+b(k，b为常数)，使得f(x)≥g(x)对一切实数x都成立，则称g(x)为函数f(x)的一个承托函数.现有如下命题：

①对给定的函数f(x)，其承托函数可能不存在，也可能有无数个；

②g(x)＝2x为函数f(x)＝2^x的一个承托函数；

③定义域和值域都是R的函数f(x)不存在承托函数.

下列选项正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.① 　　　　　　　B.②　　　　　　　 C.①③　 　　　　　　　D.②③

解析：对于①，若f(x)＝sinx，则g(x)＝B(B<－1)，就是它的一个承托函数，且有无数个，再如y＝tanx，y＝lgx就没有承托函数，∴命题①正确；

对于②，∵当x＝时，g()＝3，f()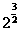＝＝2＝，∴f(x)<g(x)，

∴g(x)＝2x不是f(x)＝2^x的一个承托函数；

对于③如f(x)＝2x+3存在一个承托函数y＝2x+1.

答案：A

第Ⅱ卷　(非选择题，共100分)