
10.在极坐标系中,圆C的圆心C(6,),半径r=6.
(1)写出圆C的极坐标方程;
(2)若Q点在圆C上运动,P在OQ的延长线上,且OQ∶QP=3∶2,求动点P的轨迹方程.
解:(1)圆C的极坐标方程ρ=12cos(θ-);
(2)设P的坐标为(ρ,θ),因为P在OQ的延长线上,
即OQ∶QP=3∶2,所以点Q的坐标为(ρ,θ),
若Q点在圆C上运动,
则ρ=12cos(θ-),
即ρ=20cos(θ-),
 故点P的轨迹方程为ρ=20cos(θ-).
故点P的轨迹方程为ρ=20cos(θ-).
9.自极点O向直线l作垂线,垂足是H(2,),则直线l的极坐标方程为________.
解析:设P(ρ,θ)为直线l上任一点,则Rt△OHP中有ρcos(θ-)=2.
答案:ρcos(θ-)=2
8.在极坐标系中,若A(3,),B(-4,),则△AOB的面积等于________.
解析:点B的极坐标是(4,),在△AOB中,S△AOB=|OA||OB|·sin∠AOB=×3×4×sin=3.
答案:3
7.在同一平面直角坐标系中,直线x-2y=2经过伸缩变换后,所变成直线的方程为________.
解析:由伸缩变换
得,
将其代入x-2y=2得2x′-y′=4.
答案:2x-y=4
6.极坐标方程4ρ·sin2=5表示的曲线为 ( )
A.直线 B.圆 C.椭圆 D.抛物线
解析:4ρ·sin2=4ρ·=2ρ-2ρcosθ=5,化为直角坐标方程为2 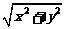 -2x=5,化简,得y2=5x+.故该方程表示抛物线.
-2x=5,化简,得y2=5x+.故该方程表示抛物线.
答案:D
5.(2009·广州模拟)在极坐标系中,直线ρsin(θ+)=2被圆ρ=4截得的弦长为 ( )
A.2 B.2 C.4 D.4
解析:直线ρsin(θ+)=2可化为x+y-2=0,
圆ρ=4可化为x2+y2=16,由圆中的弦长公式得
2=2=4.
答案:D
4.已知曲线C1,C2的极坐标方程分别为ρcosθ=3,ρ=4cosθ(ρ≥0,0≤θ<),则曲线C1 与C2交点的极坐标为 ( )
A.(2,) B.(2,) C.(2,) D.(2,)
解析:∵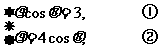
∴4cos2θ=3.∴2(1+cos2θ)=3.
∴cos2θ=.
∵0≤2θ<π,∴θ=,代入①得ρ=2.
∴C1与C2交点的极坐标为(2,).
答案:C
3.极坐标系中,曲线ρ=-4sinθ和ρcosθ=1相交于点A、B,则|AB|= ( )
A.4 B.5 C.2 D.2
解析:平面直角坐标系中,曲线ρ=-4sinθ和ρcosθ=1分别表示圆x2+(y+2)2=4和直 线x=1,作图易知|AB|=2.
答案:D
2.在极坐标系中,曲线C的方程是ρ=4sinθ,过点M(4,)作曲线C的切线,则切线长为( )
A.2 B.3 C.2 D.2
解析:∵ρ=4sinθ化为普通方程为x2+(y-2)2=4.
而点M(4,)化为直角坐标为M(2,2),
∴由勾股定理,得切线长为
=2.
即切线长为2.
答案:C
1.经过点P(2,),且垂直于极轴的直线的极坐标方程是 ( )
A.ρ=cosθ= B.ρsinθ=π
C.ρcosθ= D.ρsinθ=
解析:根据题意,所求直线为:在直角坐标系下,过点(,),垂直于x轴的直
线,方程为x=.由极坐标与直角坐标系互化公式可知x=ρcosθ,∴ρcosθ=.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com