
1.(2010·葫芦岛模拟)下列各组离子在指定环境下能大量共存的是( )。
A.pH=1的溶液中:Na+、S2-、K+、MnO4-
B.pH=7的溶液中:Al3+、Cl-、SO42-、HCO3-
C.pH>7的溶液中:Na+、AlO2-、SO42-、K+
D.pH=0的溶液中:Na+、K+、Fe2+、ClO-
[解析]选C。pH=1的溶液呈强酸性,故S2-不能存在,且在酸性条件下,MnO4- 具有强氧化性也能氧化S2-;Al3+与HCO3-相互促进水解而不能大量共存;pH=0时,溶液呈强酸性,ClO-具有强氧化性,能把Fe2+氧化成Fe3+。
 ⒈ 一个简单多面体的各面都是三角形,证明它的顶点数V和面数F有下面的关系:F=2V-4
⒈ 一个简单多面体的各面都是三角形,证明它的顶点数V和面数F有下面的关系:F=2V-4
证明:∵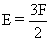 ,V+F-E=2
,V+F-E=2
∴V+F-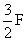 =2 ∴F=2V-4
=2 ∴F=2V-4
⒉ 设一个凸多面体有V个顶点,
求证:它的各面多边形的内角和为(V-2)·360°
解:设此多面体的上底面有V上个顶点,下底面有V下个顶点
将其下底面剪掉,抻成平面图形则
V上·360°+(V下-2)·180°+(V下-2)·180°
=(V上+V下-2)·360°
=(V-2)360°
⒊ 有没有棱数是7的简单多面体?说明理由
证明:∵V+F-E=2 , ∴V+F=7+2=9
∵多面体的顶点数V≥4,面数F≥4
∴只有两种情况V=4,F=5或V=5,F=4
但是有4个顶点的多面体只有四个面,不可能是5个面,
有四个面的多面体是四面体,也只有四个顶点,不可能有5个顶点,
∴没有棱数是7的简单多面体
⒋ 是否存在这样的多面体,它有奇数个面,且每一个面都有奇数条边
证明:设有一个多面体,有F(奇数)个面,并且每个面的边数
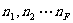 也都是奇数,则
也都是奇数,则
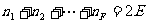
但是上式左端是奇数个“奇数相加”,结果仍为奇数,可右端是偶数,这是不可能的
∴不存在这样的多面体
例1  由欧拉定理证明:正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体这五种
由欧拉定理证明:正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体这五种
证明:设正多面体的每个面的边数为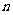 ,每个顶点连有
,每个顶点连有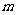 条棱,
条棱,
令这个多面体的面数为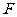 ,每个面有
,每个面有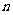 条边,故共有
条边,故共有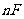 条边,由于每条边都是两个面的公共边,故多面体棱数
条边,由于每条边都是两个面的公共边,故多面体棱数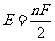 (1)
(1)
令这个多面体有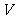 个顶点,每一个顶点处有
个顶点,每一个顶点处有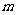 条棱,故共有
条棱,故共有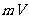 条棱
条棱 由于每条棱有两个顶点,故多面体棱数
由于每条棱有两个顶点,故多面体棱数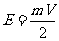 (2)
(2)
由(1)(2)得: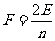 ,
,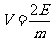 代入欧拉公式:
代入欧拉公式: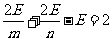 .
.
∴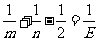 (3),
(3),
∵又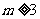 ,
,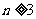 ,但
,但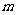 ,
,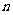 不能同时大于
不能同时大于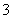 ,
,
(若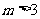 ,
,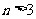 ,则有
,则有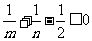 ,即
,即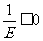 这是不可能的)
这是不可能的)
∴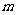 ,
,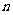 中至少有一个等于
中至少有一个等于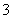 .令
.令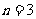 ,则
,则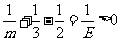 ,
,
∴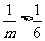 ,∴
,∴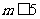 ,∴
,∴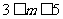 .
.
同样若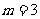 可得
可得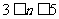 .
.
例2.欧拉定理在研究化学分子结构中的应用:
1996年诺贝尔化学奖授予对发现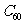 有重大贡献的三位科学家
有重大贡献的三位科学家
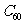 是由60个
是由60个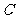 原子构成的分子,它是形如足球的多面体
原子构成的分子,它是形如足球的多面体 这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算
这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算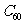 分子中五边形和六边形的数目
分子中五边形和六边形的数目
解:设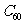 分子中有五边形
分子中有五边形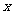 个,六边形
个,六边形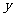 个
个
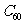 分子这个多面体的顶点数
分子这个多面体的顶点数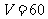 ,面数
,面数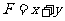 ,棱数
,棱数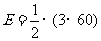 ,由欧拉定理得:
,由欧拉定理得: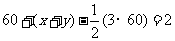 (1),
(1),
另一方面棱数可由多边形的边数和来表示,得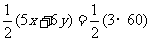 (2),由(1)(2)得:
(2),由(1)(2)得: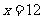 ,
,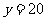
∴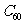 分子中五边形有12个,六边形有20个
分子中五边形有12个,六边形有20个
例3.一个正多面体各个面的内角和为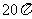 ,求它的面数、顶点数和棱数
,求它的面数、顶点数和棱数
解:由题意设每一个面的边数为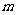 ,则
,则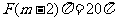 ,
,
∴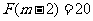 ,
,
∵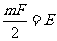 ,∴
,∴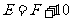 ,
,
将其代入欧拉公式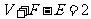 ,得
,得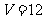 ,设过每一个顶点的棱数为
,设过每一个顶点的棱数为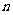 ,
,
则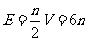 ,
,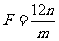 得
得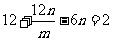 ,即
,即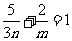 (1),
(1),
∵ ,∴
,∴ ,又
,又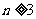 ,
,
∴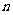 的可能取值为
的可能取值为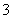 ,
,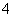 ,
,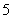 ,
,
当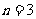 或
或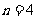 时(1)中
时(1)中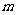 无整数解;
无整数解;
当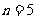 ,由(1)得
,由(1)得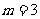 ,
,
∴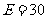 , ∴
, ∴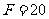 ,
,
综上可知: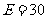 ,
,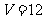 ,
,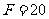 .
.
4.欧拉示性数:在欧拉公式中令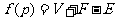 ,
,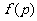 叫欧拉示性数
叫欧拉示性数
说明:(1)简单多面体的欧拉示性数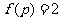 .
.
(2)带一个洞的多面体的欧拉示性数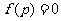 .例如:长方体挖去一个洞连结底面相应顶点得到的多面体
.例如:长方体挖去一个洞连结底面相应顶点得到的多面体

3.欧拉定理(欧拉公式):简单多面体的顶点数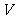 、面数
、面数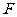 及棱数
及棱数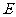 有关系式:
有关系式:
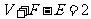 .
.
2.五种正多面体的顶点数、面数及棱数:
|
正多面体 |
顶点数 |
面数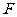 |
棱数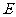 |
|
正四面体 |
4 |
4 |
6 |
|
正六面体 |
8 |
6 |
12 |
|
正八面体 |
6 |
8 |
12 |
|
正十二面体 |
20 |
12 |
30 |
|
正二十面体 |
12 |
20 |
30 |
1.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面 如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体
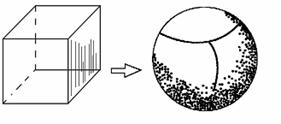
说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体
21、已知函数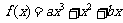 , 其中常数a,b∈R , 且
, 其中常数a,b∈R , 且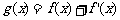 是奇函数.
是奇函数.
(Ⅰ)求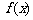 的表达式;(Ⅱ)讨论
的表达式;(Ⅱ)讨论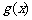 的单调性,并求
的单调性,并求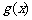 在区间
在区间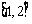 上的最大值与最小值.
上的最大值与最小值.
江西省莲塘一中2010-2011学年上学期高三年级第一次统考
20、设函数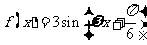 ,
, ,
,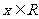 ,且以
,且以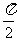 为最小正周期.
为最小正周期.
(1)求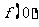 ;(2)求
;(2)求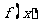 的解析式;(3)已知
的解析式;(3)已知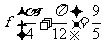 ,求
,求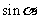 的值.
的值.
19、已知函数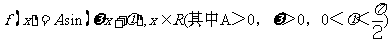 的图像与x轴的交点中,相邻两个交点之间的距离为
的图像与x轴的交点中,相邻两个交点之间的距离为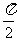 ,且图像上一个最低点为
,且图像上一个最低点为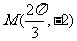 。
。
(1)求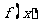 的解析式, (2)当
的解析式, (2)当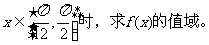
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com