
例1.用数学归纳法证明:如果{an}是一个等差数列,那么an=a1+(n-1)d对一切n∈N*都成立.
证明:(1)当n=1时,左边=a1,右边=a1+0·d=a1,等式是成立的
(2)假设当n=k时等式成立,就是ak=a1+(k-1)d.
那么ak+1=ak+d=[a1+(k-1)d]+d=a1+[(k+1)-1]d,
这就是说,当n=k+1时,等式也成立.
由(1)和(2)可以判定,等式对任何n∈N*都成立.
例2.用数学归纳法证明:1+3+5+…+(2n-1)=n2.
证明:(1)当n=1时,左边=1,右边=1,等式成立.
(2)假设当n=k时,等式成立,就是1+3+5+…+(2k-1)=k2,
那么1+3+5+…+(2k-1)+[2(k+1)-1]=k2+[2(k+1)-1]=k2+2k+1=(k+1)2.
∴n=k+1时也成立.
由(1)和(2),可知等式对任何n∈N*都成立 
6.用数学归纳法证明一个与正整数有关的命题的步骤:
(1)证明:当n取第一个值n0结论正确;
(2)假设当n=k(k∈N*,且k≥n0)时结论正确,证明当n=k+1时结论也正确.
由(1),(2)可知,命题对于从n0开始的所有正整数n都正确 
5. 数学归纳法的基本思想:即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N*)时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立.
4.数学归纳法:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;然后假设当n=k(kÎN*,k≥n0)时命题成立,证明当n=k+1时命题也成立 这种证明方法就叫做数学归纳法
这种证明方法就叫做数学归纳法
3. 完全归纳法: 把研究对象一一都考查到了而推出结论的归纳法称为完全归纳法.
完全归纳法是一种在研究了事物的所有(有限种)特殊情况后得出一般结论的推理方法,又叫做枚举法.与不完全归纳法不同,用完全归纳法得出的结论是可靠的.通常在事物包括的特殊情况数不多时,采用完全归纳法.
2. 不完全归纳法: 根据事物的部分(而不是全部)特例得出一般结论的推理方法叫做不完全归纳法.
如我们在推导涉及所有正整数的等差数列通项公式时,在考察了n=1,2,3,4几种特殊情形后得出的一般公式,就是作的一种不完全归纳.
我们已经知道,不完全归纳法所得到的命题并不能保证它成立,所以这种方法并不能作为一种论证方法;同时也应看到,不完全归纳法是研究数学的一把钥匙,是发现数学规律的一种重要手段.在问题探索中,为了寻求一般规律,往往先考察一些特例,通过对这些特例的不完全归纳形成猜想,然后再试图去证明或否定这种猜想.因而学会用不完全归纳法对问题进行探索,对提高我们的数学能力十分重要.
1. 归纳法:由一些特殊事例推出一般结论的推理方法.
特点:由特殊→一般
问题1:这里有一袋球共十二个,我们要判断这一袋球是白球,还是黑球,请问怎么办?
方法一:把它倒出来看一看就可以了.
特点:方法是正确的,但操作上缺乏顺序性.
方法二:一个一个拿,拿一个看一个.
比如结果为:第一个白球,第二个白球,第三个白球,……,第十二个白球,由此得到:这一袋球都是白球.
特点:有顺序,有过程.
问题2:在数列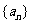 中,
中,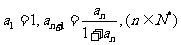 ,先算出a2,a3,a4
,先算出a2,a3,a4 的值,再推测通项an的公式.
的值,再推测通项an的公式.
过程: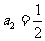 ,
,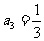 ,
,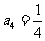 ,由此得到:
,由此得到: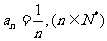 ,
,
解决以上两个问题用的都是归纳法.
再请看数学史上的两个资料:
资料1: 费马(Fermat)是17世纪法国著名的数学家,他是解析几何的发明者之一,是对微积分的创立作出贡献最多的人之一,是概率论的创始者之一,他对数论也有许多贡献.但是,费马曾认为,当n∈N时,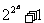 一定都是质数,这是他对n=0,1,2,3,4时的值分别为3,5,17,257,65537作了验证后得到的.
一定都是质数,这是他对n=0,1,2,3,4时的值分别为3,5,17,257,65537作了验证后得到的.
18世纪伟大的瑞士科学家欧拉(Euler)却证明了当n=5时,
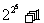 =4 294 967 297=6
700 417×641,从而否定了费马的推测.
=4 294 967 297=6
700 417×641,从而否定了费马的推测.
有人说,费马为什么不再多算一个数呢?今天我们是无法回答的.但是要告诉同学们,失误的关键不在于多算一个上!
资料2:f(n)=n2+n+41,当n∈N时,f(n)是否都为质数?
f(0)=41,f(1)=43,f(2)=47,f(3)=53,f(4)=61,
f(5)=71,f(6)=83,f(7)=97,f(8)=113,f(9)=131,
f(10)=151,… f(39)=1 601.
但是f(40)=1 681=412是合数
算了39个数不算少了吧,但还不行!我们介绍以上两个资料,不是说世界级大师还出错,我们有错就可以原谅,也不是说归纳法不行,不去学了,而是要找出运用归纳法出错的原因,并研究出对策来.
对于生活、生产中的实际问题,得出的结论的正确性,应接受实践的检验,因为实践是检验真理的唯一标准.对于数学问题,应寻求数学证明

课件展示:多媒体课件(游戏:多米诺骨牌) ,多米诺骨牌游戏要取得成功,必须靠两条:
(1)骨牌的排列,保证前一张牌倒则后一张牌也必定倒;
(2)第一张牌被推倒.
用这种思想设计出来的,用于证明不完全归纳法推测所得命题的正确性的证明方法就是数学归纳法.
23.(2010·宜宾模拟)某强酸性溶液X,含有Ba2+、Al3+、SiO32-、NH4+、Fe2+、Fe3+、
CO32-、SO42-、NO3-中的一种或几种离子,取溶液进行连续实验,能实现如下转化:
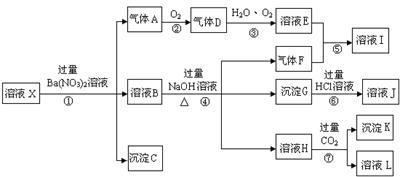
依据以上信息,回答下列问题:
(1)上述离子中,溶液X中肯定含有的是:_____________________________;不能肯定的是:_________________。对不能确定是否存在的离子,可以另取X溶液于一支试管中,选择下列试剂中的一种加入X溶液中,根据现象就可判断,则该试剂是:___________。(选填:①NaOH溶液,②酚酞试剂,③石蕊试剂,④pH试纸,⑤KSCN溶液,⑥KMnO4溶液)
(2)气体F的化学式为:_______________,沉淀G的化学式为:_____________,沉淀K的化学式为:____________,实验中,可以观察到反应②的现象是:________________。
(3)写出步骤①所有发生反应的离子方程式_________________、__________________。
(4)要使步骤③中,D、H2O、O2三种物质恰好发生化合反应,则D、H2O、O2物质的量之比是:______________________。
[解析]强酸性溶液中含有H+,则不含SiO32-、CO32-;加入Ba(NO3)2溶液后生成的沉淀一定是BaSO4,则溶液中含有SO42-,不含Ba2+;气体A能够和氧气反应,所以A为NO,D为NO2,D到E的反应为:4NO2+O2+2H2O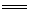 4HNO3,说明该溶液中含有还原性离子,即Fe2+,则原溶液中一定没有NO3-。溶液B能够和NaOH溶液反应生成气体,则该气体一定是NH3,原溶液中一定含有NH4+。符合转化关系:“B
4HNO3,说明该溶液中含有还原性离子,即Fe2+,则原溶液中一定没有NO3-。溶液B能够和NaOH溶液反应生成气体,则该气体一定是NH3,原溶液中一定含有NH4+。符合转化关系:“B H
H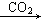 沉淀K”的K为Al(OH)3,则溶液中含有Al3+。
沉淀K”的K为Al(OH)3,则溶液中含有Al3+。
[答案](1)SO42-、Al3+、Fe2+、NH4+ Fe3+ ⑤
(2)NH3 Fe(OH)3 Al(OH)3 气体由无色变成红棕色
(3)Ba2++SO42-=BaSO4↓ 3Fe2++NO3-+4H+=3Fe3++NO↑+2H2O
(4)4∶2∶1
()
22.(2010·锦州模拟)已知A和B两支试管的溶液中共含有K+、Ag+、Mg2+、Cl-、OH-、NO3-六种离子,向试管A的溶液中滴入酚酞试液呈粉红色。请回答下列问题:
(1)试管A的溶液中所含上述离子共有______种。
(2)若向某试管中滴入稀盐酸产生沉淀,则该试管为______(填“A”或“B”)。
(3)若向试管B的溶液中加入合适的药品,过滤后可以得到相应的金属和仅含一种溶质的溶液,则加入的药品是___________(填化学式)。
(4)若将试管A和试管B中的溶液按一定体积比混合过滤后,蒸干滤液可得到一种纯净物,则混合过程中发生反应的离子方程式为_______________、________________。
(5)若试管A和试管B中共有四种物质按等物质的量溶解于试管中,再将A和B中的溶液混合过滤,所得滤液中各种离子的物质的量之比为________________。
(6)若向由试管A的溶液中阳离子组成的碳酸氢盐溶液中,滴入少量Ba(OH)2溶液,则发生反应的离子方程式为______________________________。
[解析]酚酞试液呈粉红色,说明试管A溶液中含有OH-,则没有能够和OH-结合成沉淀的离子,所以Ag+、Mg2+不存在,它们一定在试管B中,根据电荷守恒,则必定存在K+;Cl-能够和Ag+结合成AgCl沉淀,在B中不含Cl-,根据电荷守恒,B中所含的阴离子一定是NO3-。综上所述,A中含有K+、Cl-和OH-三种离子,B中含有Ag+、Mg2+和NO3-三种离子。然后结合题目要求即得答案。
[答案](1)3 (2)B (3)Mg
(4)Ag+ +Cl-=AgCl↓、Mg2++2OH-=Mg(OH)2↓
(5)n (K+)︰n (Mg2+)︰n (NO3-)=4︰1︰6
(6)Ba2++2OH-+2HCO3-=BaCO3↓+CO32-+2H2O
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com