5．给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：

①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；

②“若a，b，c，d∈R，则复数a+bi＝c+di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a+b＝c+d⇒a＝c，b＝d”；

③“若a，b∈R，则a－b＞0⇒a＞b”类比推出“若a，b∈C，则a－b＞0⇒a＞b”．

其中类比得到的结论正确的个数是　　　　　　　　　　　　　　　　　　　 (　)

A．0　 　　　　　　B．1 　　　　　　C．2 　　　　　　　　D．3

解析：①②是正确的，③是错误的，因为复数不能比较大小，如a＝5+6i，b＝4+6i，虽然满足a－b＝1＞0，但复数a与b不能比较大小．

答案：C

4．若集合A＝{x||2x－1|＜3}，B＝{x|＜0}，则A∩B是　　　　　　　　　 (　)

A．{x|－1＜x＜－或2＜x＜3}　　　　 B．{x|2＜x＜3}

C．{x|－＜x＜2}　　　　　　　　　 　D．{x|－1＜x＜－}

解析：∵|2x－1|＜3，∴－3＜2x－1＜3.∴－1＜x＜2.

又∵＜0，∴(2x+1)(x－3)＞0，

∴x＞3或x＜－.∴A∩B＝{x|－1＜x＜－}．

答案：D

3．已知函数f(x)＝，若f(x)≥1，则x的取值范围是　　　　　　 (　)

A．(－∞，－1]　 　　　　　　　B．[1，+∞)

C．(－∞，0]∪[1，+∞) 　　　　D．(－∞，－1]∪[1，+∞)

解析：将原不等式转化为：或，从而得x≥1或x≤－1.

答案：D

2．下列命题中的真命题是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若a＞b，c＞d，则ac＞bd　 　　　B．若|a|＞b，则a²＞b²

C．若a＞b，则a²＞b²　 　　　　　　D．若a＞|b|，则a²＞b²

解析：由a＞|b|，可得a＞|b|≥0⇒a²＞b².

答案：D

1．不等式(x+1)≥0的解集是　　　　　　　　　　　　　　　　　　　　 (　)

A．{x|x＞1}　　　　B．{x|x≥1}

C．{x|x≥1或x＝－1} 　　　D．{x|x≥－1或x＝1}

解析：∵≥0，∴x≥1.

同时x+1≥0，即x≥－1.∴x≥1.

答案：B

21．(2010·东北四市模拟)已知O为坐标原点，点A、B分别在x轴，y轴上运动，且|AB|＝8，动点P满足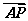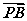＝，设点P的轨迹为曲线C，定点为M(4,0)，直线PM交曲线C于另外一点Q.

(1)求曲线C的方程；

(2)求△OPQ面积的最大值．

解：(1)设A(a,0)，B(0，b)，P(x，y)，

则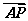＝(x－a，y)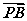，＝(－x，b－y)，

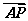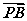∵＝，∴∴a＝x，b＝y.

又|AB|＝＝8，∴+＝1.

∴曲线C的方程为+＝1.

(2)由(1)可知，M(4,0)为椭圆+＝1的右焦点，

设直线PM方程为x＝my+4，

由消去x得

(9m²+25)y²+72my－81＝0，

∴|y_P－y_Q|＝

＝.

∴S_△OPQ＝|OM||y_P－y_Q|＝2×

＝＝＝

≤＝，

当＝，

即m＝±时，△OPQ的面积取得最大值为，此时直线方程为3x±y－12＝0.

20．已知A、B、D三点不在一条直线上，且A(－2,0)，B(2,0)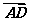，||＝2，＝(+)．

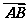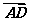(1)求E点的轨迹方程；

(2)过A作直线交以A、B为焦点的椭圆于M，N两点，线段MN的中点到y轴的距离为，且直线MN与E点的轨迹相切，求椭圆的方程．

解：(1)设E(x，y)，由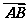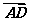＝(+)，可知E为线段BD的中点，

又因为坐标原点O为线段AB的中点，

所以OE是△ABD的中位线，

所以|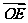|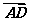＝||＝1，

所以E点在以O为圆心，1为半径的圆上，

又因为A，B，D三点不在一条直线上，

所以E点不能在x轴上，

所以E点的轨迹方程是x²+y²＝1(y≠0)．

(2)设M(x₁，y₁)，N(x₂，y₂)，中点为(x₀，y₀)，椭圆的方程为+＝1，直线MN的方程为y＝k(x+2)(当直线斜率不存在时不成立)，

由于直线MN与圆x²+y²＝1(y≠0)相切，

所以＝1，解得k＝±，

所以直线MN的方程为y＝±(x+2)，

将直线y＝±(x+2)代入方程+＝1，

整理可得：4(a²－3)x²+4a²x+16a²－3a⁴＝0，

所以x₀＝＝－.

又线段MN的中点到y轴的距离为，

即x₀＝－＝－，解得a＝2.

故所求的椭圆方程为+＝1.

19．给定抛物线C：y²＝4x，F是C的焦点，过点F的直线l与C相交于A，B两点，记O为坐标原点．

(1)求·的值；

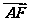(2)设＝λ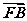，当△OAB的面积S∈[2， ]时，求λ的取值范围．

解：(1)根据抛物线的方程可得焦点F(1,0)，

设直线l的方程为x＝my+1，

将其与C的方程联立，消去x可得y²－4my－4＝0.

设A，B点的坐标分别为(x₁，y₁)，(x₂，y₂)(y₁>0>y₂)，

则y₁y₂＝－4.

因为y＝4x₁，y＝4x₂，

所以x₁x₂＝yy＝1，

故·＝x₁x₂+y₁y₂＝－3.

(2)因为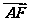＝λ，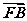

所以(1－x₁，－y₁)＝λ(x₂－1，y₂)，

即

又y＝4x₁，　　　　　　　　　　　　　　　　　　 ③

y＝4x₂，　　　　　　　　　　　　　　　　　　　 ④

由②③④消去y₁，y₂后，得到x₁＝λ²x₂，将其代入①，注意到λ>0，解得x₂＝.从而可得y₂＝－，y₁＝2，

故△OAB的面积S＝|OF|·|y₁－y₂|＝+，

因+≥2恒成立，所以只要解+≤即可，

解之得≤λ≤.

18． (2010·南通模拟)已知动圆过定点F(0,2)，且与定直线L：y＝－2相切．

(1)求动圆圆心的轨迹C的方程；

(2)若AB是轨迹C的动弦，且AB过F(0,2)，分别以A、B为切点作轨迹C的切线，设两切线交点为Q，证明：AQ⊥BQ.

解：(1)依题意，圆心的轨迹是以F(0,2)为焦点，L：y＝－2为准线的抛物线．

因为抛物线焦点到准线距离等于4，

所以圆心的轨迹是x²＝8y.

(2)证明：因为直线AB与x轴不垂直，

设AB：y＝kx+2.

A(x₁，y₁)，B(x₂，y₂)．

由

可得x²－8kx－16＝0，x₁+x₂＝8k，x₁x₂＝－16.

抛物线方程为y＝x²，求导得y′＝x.

所以过抛物线上A、B两点的切线斜率分别是k₁＝x₁，k₂＝x₂，k₁k₂＝x₁·x₂＝x₁·x₂＝－1.

所以AQ⊥BQ.

17．过点P(2,4)作两条互相垂直的直线l₁、l₂，若l₁交x轴于A点，l₂交y轴于B点，求线段AB的中点M的轨迹方程．

解：设M的坐标为(x，y)，则A、B两点的坐标分别是(2x,0)，(0,2y)，

连结PM，

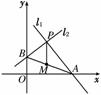∵l₁⊥l₂，∴2|PM|=|AB|.

而|PM|=，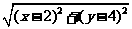

|AB|=,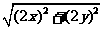

∴2.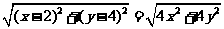

化简，得x+2y-5=0即为所求的轨迹方程．