
4、设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为 ( )
A.15 B.10 C.20 D.5
3、如果随机变量ξ-B(n,p),且Eξ=7,Dξ=6,则p等于 ( )
A.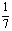 B.
B.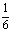 C.
C.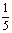 D.
D.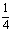
2、随机变量ξ的分布列为P(ξ=k)=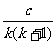 ,k=1、2、3、4,c为常数,则P(
,k=1、2、3、4,c为常数,则P(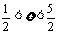 )的值为
(
)
)的值为
(
)
A.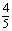 B.
B.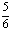 C.
C.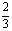 D.
D.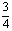
1、为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为 ( )
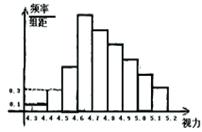
A.0.27,78
B.0.27,83
C.2.7,78
D.2.7,83
100. 已知二次函数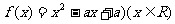 同时满足:①不等式
同时满足:①不等式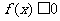 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在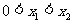 ,使得不等式
,使得不等式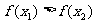 成立。设数列
成立。设数列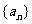 的前n项和
的前n项和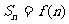 。
。
(1)求函数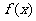 的表达式;
的表达式;
(2)求数列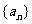 的通项公式;
的通项公式;
(3)设各项均不为零的数列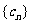 中,所有满足
中,所有满足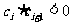 的整数I的个数称为这个数列
的整数I的个数称为这个数列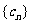 的变号数。令
的变号数。令 (n为正整数),求数列
(n为正整数),求数列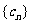 的变号数.
的变号数.
99.已知⊙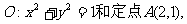 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足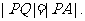
(1)求实数a,b间满足的等量关系; (2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
98.如图所示,在棱长为2的正方体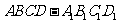 中,
中,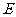 、
、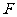 分别为
分别为 、
、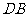 的中点.
的中点.
|
|
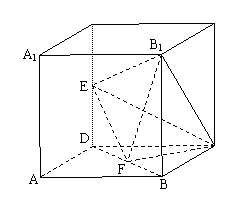 (1)求证:
(1)求证: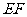 //平面
//平面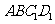 ;
;
(2)求证: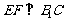 ;
;
(3)求三棱锥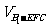 的体积.
的体积.
|
97、已知定义域为R的二次函数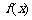 的最小值为0且有
的最小值为0且有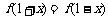 ,直线
,直线 被
被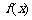 的图像截得的弦长为
的图像截得的弦长为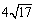 ,数列
,数列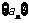 满足
满足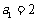 ,
,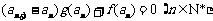 .
.
(1)函数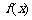 ;(2)求数列
;(2)求数列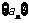 的通项公式;
的通项公式;
(3)设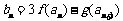 ,求数列
,求数列 的最值及相应的n.
的最值及相应的n.
96、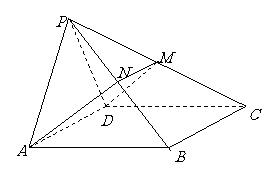 如图,在四棱锥
如图,在四棱锥 中,侧面
中,侧面 是正三角形,且与底面
是正三角形,且与底面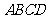 垂直,底面
垂直,底面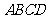 是边长为
是边长为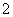 的菱形,
的菱形,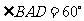 ,
,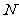 是
是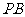 中点,截面
中点,截面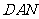 交
交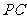 于
于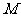 .
.
(1)求证: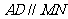 ;
;
(2)求证: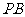 ⊥平面
⊥平面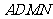 ;
;
(3)求三棱锥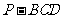 的体积.
的体积.
95、已知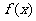 是二次函数,不等式
是二次函数,不等式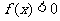 的解集是
的解集是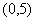 ,且
,且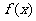 在区间
在区间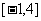 上的最大值是12。
上的最大值是12。
(1)求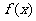 的解析式;
的解析式;
(2)是否存在实数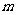 ,使得方程
,使得方程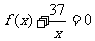 在区间
在区间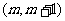 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出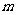 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com