
5、(07广东文)已知抛物线关于x轴对称,顶点在原点O,且过点P(2,4),则该抛物线的方程是
[解析]设所求抛物线方程为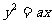 ,依题意
,依题意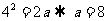 ,故所求为
,故所求为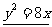 .
.
(07广东理)在直角坐标系xOy中,有一定点A(2,1)。若线段OA的垂直平分线过抛物线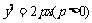 的焦点,则该抛物线的准线方程是_____________。
的焦点,则该抛物线的准线方程是_____________。
答案: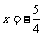 ;
;
解析:OA的垂直平分线的方程是y-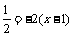 ,令y=0得到x=
,令y=0得到x=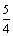 .
.
4、(07宁海文)已知 是等差数列,
是等差数列,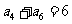 ,其前5项和
,其前5项和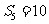 ,则其公差
,则其公差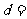
[答案]: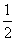
[分析]: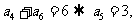
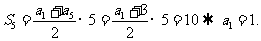
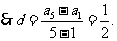
(07宁海理)某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 种(用数字作答)
[答案]:240
[分析]:由题意可知有一个工厂安排2个班,另外三个工厂每厂一个班,
共有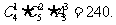 种安排方法。
种安排方法。
3、(07宁海文)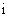 是虚数单位,
是虚数单位,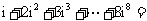 (用
(用 的形式表示,
的形式表示,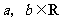 )
)
[答案]:
[分析]: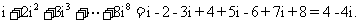
(07宁海理)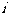 是虚数单位,(-5+10i)/(3+4i)= (用
是虚数单位,(-5+10i)/(3+4i)= (用 的形式表示,
的形式表示,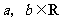 )
)
[答案]:
[分析]: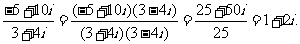
2、(07宁海文)设函数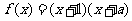 为偶函数,则
为偶函数,则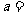
[答案]:-1
[分析]: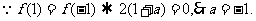
(07宁海理)设函数f(x)=[(x+1)(x+a)]/x为奇函数,则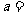
[答案]:-1
[分析]: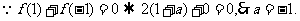
1、(07宁海)双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为
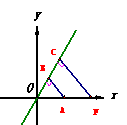 [答案]:3
[答案]:3
[分析]:如图,过双曲线的顶点A、焦点F分别
向其渐近线作垂线,垂足分别为B、C,
则: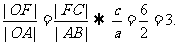
11.
一只酒杯的轴截面是抛物线的一部分,它的函数解析式是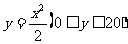 ,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
,在杯内放一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的取值范围是___________.
讲解 依抛物线的对称性可知,大圆的圆心在y轴上,并且圆与抛物线切于抛物线的顶点,从而可设大圆的方程为 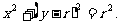
由
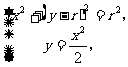
消去x,得 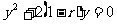 (*)
(*)
解出 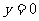 或
或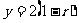
要使(*)式有且只有一个实数根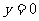 ,只要且只需要
,只要且只需要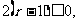 即
即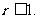
再结合半径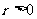 ,故应填
,故应填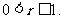
高考题选:
10. 椭圆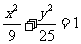 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解
记椭圆的二焦点为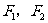 ,有
,有
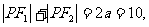
则知
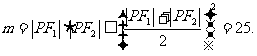
显然当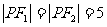 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填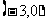 或
或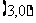
9.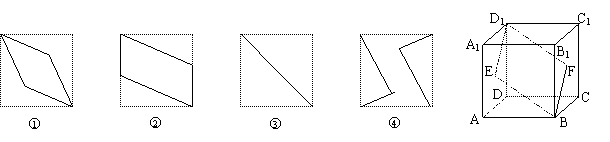 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
8. 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径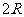 , 即有
, 即有
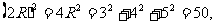
从而 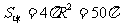 ,故应填
,故应填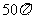
7. 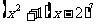 的展开式中
的展开式中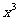 的系数是
的系数是
讲解 由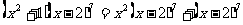 知,所求系数应为
知,所求系数应为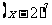 的x项的系数与
的x项的系数与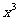 项的系数的和,即有
项的系数的和,即有
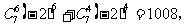
故应填1008.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com