
1.做匀速圆周运动物体所受的合力为向心力
“向心力”是一种效果力。任何一个力,或者几个力的合力,或者某一个力的某个分力,只要其效果是使物体做匀速圆周运动的,都可以作为向心力。
在应用牛顿第二定律解题时,有时为了方便,可以取一组物体(一组质点)为研究对象。这一组物体一般具有相同的速度和加速度,但也可以有不同的速度和加速度。以质点组为研究对象的好处是可以不考虑组内各物体间的相互作用,这往往给解题带来很大方便。使解题过程简单明了。
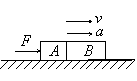 例5. 如图所示,A、B两木块的质量分别为mA、mB,在水平推力F作用下沿光滑水平面匀加速向右运动,求A、B间的弹力FN。
例5. 如图所示,A、B两木块的质量分别为mA、mB,在水平推力F作用下沿光滑水平面匀加速向右运动,求A、B间的弹力FN。
解:这里有a、FN两个未知数,需要要建立两个方程,要取两次研究对象。比较后可知分别以B、(A+B)为对象较为简单(它们在水平方向上都只受到一个力作用)。可得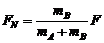
这个结论还可以推广到水平面粗糙时(A、B与水平面间μ相同);也可以推广到沿斜面方向推A、B向上加速的问题,有趣的是,答案是完全一样的。
 例6. 如图,倾角为α的斜面与水平面间、斜面与质量为m的木块间的动摩擦因数均为μ,木块由静止开始沿斜面加速下滑时斜面始终保持静止。求水平面给斜面的摩擦力大小和方向。
例6. 如图,倾角为α的斜面与水平面间、斜面与质量为m的木块间的动摩擦因数均为μ,木块由静止开始沿斜面加速下滑时斜面始终保持静止。求水平面给斜面的摩擦力大小和方向。
解:以斜面和木块整体为研究对象,水平方向仅受静摩擦力作用,而整体中只有木块的加速度有水平方向的分量。可以先求出木块的加速度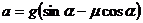 ,再在水平方向对质点组用牛顿第二定律,很容易得到:
,再在水平方向对质点组用牛顿第二定律,很容易得到: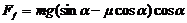
如果给出斜面的质量M,本题还可以求出这时水平面对斜面的支持力大小为:
FN=Mg+mg(cosα+μsinα)sinα,这个值小于静止时水平面对斜面的支持力。
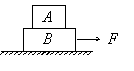 例7. 如图所示,mA=1kg,mB=2kg,A、B间静摩擦力的最大值是5N,水平面光滑。用水平力F拉B,当拉力大小分别是F=10N和F=20N时,A、B的加速度各多大?
例7. 如图所示,mA=1kg,mB=2kg,A、B间静摩擦力的最大值是5N,水平面光滑。用水平力F拉B,当拉力大小分别是F=10N和F=20N时,A、B的加速度各多大?
解:先确定临界值,即刚好使A、B发生相对滑动的F值。当A、B间的静摩擦力达到5N时,既可以认为它们仍然保持相对静止,有共同的加速度,又可以认为它们间已经发生了相对滑动,A在滑动摩擦力作用下加速运动。这时以A为对象得到a =5m/s2;再以A、B系统为对象得到 F =(mA+mB)a =15N
⑴当F=10N<15N时, A、B一定仍相对静止,所以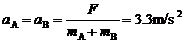
⑵当F=20N>15N时,A、B间一定发生了相对滑动,用质点组牛顿第二定律列方程: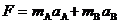 ,而a A =5m/s2,于是可以得到a B =7.5m/s2
,而a A =5m/s2,于是可以得到a B =7.5m/s2
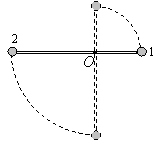 例8. 长L的轻杆两端分别固定有质量为m的小铁球,杆的三等分点O处有光滑的水平转动轴。用手将该装置固定在杆恰好水平的位置,然后由静止释放,当杆到达竖直位置时,求轴对杆的作用力F的大小和方向。
例8. 长L的轻杆两端分别固定有质量为m的小铁球,杆的三等分点O处有光滑的水平转动轴。用手将该装置固定在杆恰好水平的位置,然后由静止释放,当杆到达竖直位置时,求轴对杆的作用力F的大小和方向。
解:根据系统机械能守恒可求出小球1在最高点的速度v:mgžBL=mgž2L+1mv2+1m(2v)2, 在竖直位置对系统用牛顿第二定律,以向下为正方向,设轴对系统的作用力F向上, ,得到F=2.4mg
,得到F=2.4mg
3.应用举例
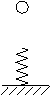 例1. 如图所示,如图所示,轻弹簧下端固定在水平面上。一个小球从弹簧正上方某一高度处由静止开始自由下落,接触弹簧后把弹簧压缩到一定程度后停止下落。在小球下落的这一全过程中,下列说法中正确的是
例1. 如图所示,如图所示,轻弹簧下端固定在水平面上。一个小球从弹簧正上方某一高度处由静止开始自由下落,接触弹簧后把弹簧压缩到一定程度后停止下落。在小球下落的这一全过程中,下列说法中正确的是
A.小球刚接触弹簧瞬间速度最大
B.从小球接触弹簧起加速度变为竖直向上
C.从小球接触弹簧到到达最低点,小球的速度先增大后减小
D.从小球接触弹簧到到达最低点,小球的加速度先减小后增大
 解:小球的加速度大小决定于小球受到的合外力。从接触弹簧到到达最低点,弹力从零开始逐渐增大,所以合力先减小后增大,因此加速度先减小后增大。当合力与速度同向时小球速度增大,所以当小球所受弹力和重力大小相等时速度最大。选CD。
解:小球的加速度大小决定于小球受到的合外力。从接触弹簧到到达最低点,弹力从零开始逐渐增大,所以合力先减小后增大,因此加速度先减小后增大。当合力与速度同向时小球速度增大,所以当小球所受弹力和重力大小相等时速度最大。选CD。
例2. 如图所示, m =4kg的小球挂在小车后壁上,细线与竖直方向成37°角。求:⑴小车以a=g向右加速;⑵小车以a=g向右减速时,细线对小球的拉力F1和后壁对小球的压力F2各多大?
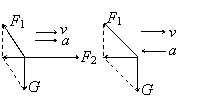 解:⑴向右加速时小球对后壁必然有压力,球在三个共点力作用下向右加速。合外力向右,F2向右,因此G和F1的合力一定水平向左,所以 F1的大小可以用平行四边形定则求出:F1=50N,可见向右加速时F1的大小与a无关;F2可在水平方向上用牛顿第二定律列方程:F2-0.75G =ma计算得F2=70N。可以看出F2将随a的增大而增大。(这种情况下用平行四边形定则比用正交分解法简单。)
解:⑴向右加速时小球对后壁必然有压力,球在三个共点力作用下向右加速。合外力向右,F2向右,因此G和F1的合力一定水平向左,所以 F1的大小可以用平行四边形定则求出:F1=50N,可见向右加速时F1的大小与a无关;F2可在水平方向上用牛顿第二定律列方程:F2-0.75G =ma计算得F2=70N。可以看出F2将随a的增大而增大。(这种情况下用平行四边形定则比用正交分解法简单。)
 ⑵必须注意到:向右减速时,F2有可能减为零,这时小球将离开后壁而“飞”起来。这时细线跟竖直方向的夹角会改变,因此F1的方向会改变。所以必须先求出这个临界值。当时G和F1的合力刚好等于ma,所以a的临界值为
⑵必须注意到:向右减速时,F2有可能减为零,这时小球将离开后壁而“飞”起来。这时细线跟竖直方向的夹角会改变,因此F1的方向会改变。所以必须先求出这个临界值。当时G和F1的合力刚好等于ma,所以a的临界值为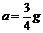 。当a=g时小球必将离开后壁。不难看出,这时F1=
。当a=g时小球必将离开后壁。不难看出,这时F1=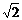 mg=56N, F2=0
mg=56N, F2=0
例3. 如图所示,在箱内倾角为α的固定光滑斜面上用平行于斜面的细线固定一质量为m的木块。求:⑴箱以加速度a匀加速上升,⑵箱以加速度a向左匀加速运动时,线对木块的拉力F1和斜面对箱的压力F2各多大?
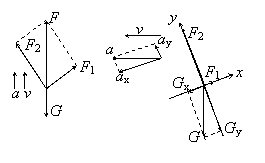 解:⑴a向上时,由于箱受的合外力竖直向上,重力竖直向下,所以F1、F2的合力F必然竖直向上。可先求F,再由F1=Fsinα和F2=Fcosα求解,得到: F1=m(g+a)sinα,F2=m(g+a)cosα
解:⑴a向上时,由于箱受的合外力竖直向上,重力竖直向下,所以F1、F2的合力F必然竖直向上。可先求F,再由F1=Fsinα和F2=Fcosα求解,得到: F1=m(g+a)sinα,F2=m(g+a)cosα
显然这种方法比正交分解法简单。
⑵a向左时,箱受的三个力都不和加速度在一条直线上,必须用正交分解法。可选择沿斜面方向和垂直于斜面方向进行正交分解,(同时正交分解a),然后分别沿x、y轴列方程求F1、F2:
F1=m(gsinα-acosα),F2=m(gcosα+asinα)
经比较可知,这样正交分解比按照水平、竖直方向正交分解列方程和解方程都简单。
还应该注意到F1的表达式F1=m(gsinα-acosα)显示其有可能得负值,这意味这绳对木块的力是推力,这是不可能的。这里又有一个临界值的问题:当向左的加速度a≤gtanα时F1=m(gsinα-acosα)沿绳向斜上方;当a>gtanα时木块和斜面不再保持相对静止,而是相对于斜面向上滑动,绳子松弛,拉力为零。
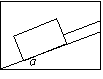
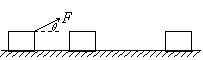 例4. 如图所示,质量m=4kg的物体与地面间的动摩擦因数为μ=0.5,在与水平成θ=37°角的恒力F作用下,从静止起向右前进t1=2.0s后撤去F,又经过t2=4.0s物体刚好停下。求:F的大小、最大速度vm、总位移s。
例4. 如图所示,质量m=4kg的物体与地面间的动摩擦因数为μ=0.5,在与水平成θ=37°角的恒力F作用下,从静止起向右前进t1=2.0s后撤去F,又经过t2=4.0s物体刚好停下。求:F的大小、最大速度vm、总位移s。
解:由运动学知识可知:前后两段匀变速直线运动的加速度a与时间t成反比,而第二段中μmg=ma2,加速度a2=μg=5m/s2,所以第一段中的加速度一定是a1=10m/s2。再由方程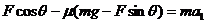 可求得:F=54.5N
可求得:F=54.5N
第一段的末速度和第二段的初速度相等都是最大速度,可以按第二段求得:vm=a2t2=20m/s 又由于两段的平均速度和全过程的平均速度相等,所以有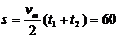 m
m
需要引起注意的是:在撤去拉力F前后,物体受的摩擦力发生了改变。
3.应用牛顿第二定律解题的步骤
①明确研究对象。可以以某一个物体为对象,也可以以几个物体组成的质点组为对象。设每个质点的质量为mi,对应的加速度为ai,则有:F合=m1a1+m2a2+m3a3+……+mnan
对这个结论可以这样理解:先分别以质点组中的每个物体为研究对象用牛顿第二定律:
∑F1=m1a1,∑F2=m2a2,……∑Fn=mnan,将以上各式等号左、右分别相加,其中左边所有力中,凡属于系统内力的,总是成对出现并且大小相等方向相反的,其矢量和必为零,所以最后得到的是该质点组所受的所有外力之和,即合外力F。
②对研究对象进行受力分析。同时还应该分析研究对象的运动情况(包括速度、加速度),并把速度、加速度的方向在受力图旁边画出来。
③若研究对象在不共线的两个力作用下做加速运动,一般用平行四边形定则(或三角形定则)解题;若研究对象在不共线的三个以上的力作用下做加速运动,一般用正交分解法解题(注意灵活选取坐标轴的方向,既可以分解力,也可以分解加速度)。
④当研究对象在研究过程的不同阶段受力情况有变化时,那就必须分阶段进行受力分析,分阶段列方程求解。
解题要养成良好的习惯。只要严格按照以上步骤解题,同时认真画出受力分析图,标出运动情况,那么问题都能迎刃而解。
2.牛顿第二定律确立了力和运动的关系
牛顿第二定律明确了物体的受力情况和运动情况之间的定量关系。联系物体的受力情况和运动情况的桥梁或纽带就是加速度。
1.定律的表述
物体的加速度跟所受的外力的合力成正比,跟物体的质量成反比,加速度的方向跟合力的方向相同,既F=ma (其中的F和m、a必须相对应)特别要注意表述的第三句话。因为力和加速度都是矢量,它们的关系除了数量大小的关系外,还有方向之间的关系。明确力和加速度方向,也是正确列出方程的重要环节。
若F为物体受的合外力,那么a表示物体的实际加速度;若F为物体受的某一个方向上的所有力的合力,那么a表示物体在该方向上的分加速度;若F为物体受的若干力中的某一个力,那么a仅表示该力产生的加速度,不是物体的实际加速度。
2.一对作用力和反作用力的冲量和功
一对作用力和反作用力在同一个过程中(同一段时间或同一段位移)的总冲量一定为零,但作的总功可能为零、可能为正、也可能为负。这是因为作用力和反作用力的作用时间一定是相同的,而位移大小、方向都可能是不同的。
1.区分一对作用力反作用力和一对平衡力
一对作用力反作用力和一对平衡力的共同点有:大小相等、方向相反、作用在同一条直线上。不同点有:作用力反作用力作用在两个不同物体上,而平衡力作用在同一个物体上;作用力反作用力一定是同种性质的力,而平衡力可能是不同性质的力;作用力反作用力一定是同时产生同时消失的,而平衡力中的一个消失后,另一个可能仍然存在。
3.牛顿第一定律描述的是理想化状态
牛顿第一定律描述的是物体在不受任何外力时的状态。而不受外力的物体是不存在的。物体不受外力和物体所受合外力为零是有区别的,所以不能把牛顿第一定律当成牛顿第二定律在F=0时的特例。
2.牛顿第一定律导出了惯性的概念
一切物体都有保持原有运动状态的性质,这就是惯性。惯性反映了物体运动状态改变的难易程度(惯性大的物体运动状态不容易改变)。质量是物体惯性大小的量度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com