
21、(本小题12分)设函数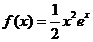 .
.
(1)求函数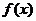 的单调区间;
的单调区间;
(2)若当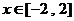 时,不等式恒
时,不等式恒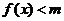 成立,求实数m的取值范围.
成立,求实数m的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。作答时先写清楚所选题目的题号。
[解](1)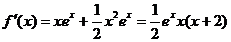 ,
,
令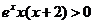 ,得
,得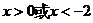 ,
,
∴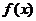 的增区间为
的增区间为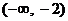 和
和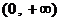 ,………3分
,………3分
令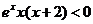 ,得
,得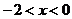 ,
,
 ∴
∴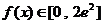 ,
……………………………………………………………11分
,
……………………………………………………………11分
∴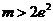 .
………………………………………………………………………12分
.
………………………………………………………………………12分
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所作的第一题记分。作答时先写清楚所选题目的题号。
19、(本小题12分)已知函数f ( x ) =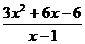 。
。
(Ⅰ)求函数f ( x
)在点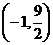 处的切线方程;
处的切线方程;
(Ⅱ)求函数f ( x )的极大值和极小值。

况如下表:
|
x |
(-∞,0) |
0 |
( 0 , 1 ) ,
(1 , 2 ) |
2 |
( 2 , +∞ ) |
|
f′( x ) |
+ |
0 |
– |
0 |
+ |
………… 9分
所以当x = 0时,函数f ( x )取得极大值为6;当x = 2时,函数f ( x )取得极小值为18。
………… 12分
18、(本小题12分)
已知集合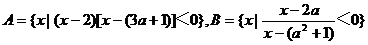 ,其中a≠1
,其中a≠1
(1)当a=2时,求A∩B; (2)求使B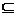 A的实数a的取值范围。
A的实数a的取值范围。
解析:(1)当a=2时,A=(2,7),B=(4,5)
∴A∩B=(4,5) ················4分
(2)∵B=(2a,a2+1)
当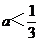 时,A=(3a+1,2)要使
时,A=(3a+1,2)要使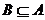 ,必须
,必须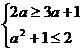 ,此时a=-1; ···6分
,此时a=-1; ···6分
当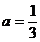 时,
时,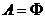 ,使
,使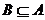 的a不存在; ···8分
的a不存在; ···8分
当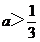 时,A=(2,3a+1)要使
时,A=(2,3a+1)要使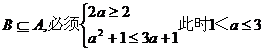
综上可知,使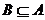 ,的实数a的取值范围
,的实数a的取值范围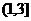 ················12分
················12分
17、(本小题12分)
已知函数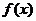 对一切
对一切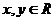 都有
都有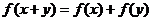
(1)试判断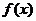 的奇偶性;
的奇偶性;
(2)若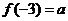 ,用
,用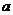 表示
表示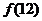 .
.
的最大
奇;-4a
16、对于函数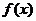 ,在使
,在使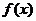 ≥M恒成立的所有常数M中,我们把M中的最大值称为函数
≥M恒成立的所有常数M中,我们把M中的最大值称为函数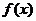 的“下确界”,则函数
的“下确界”,则函数 的下确界为 0.5 .
的下确界为 0.5 .
15、在实数集中定义一种运算“*”,具有性质: 1)a*b=b*a 2) a*0=a
3) (a*b)*c=c*(ab)+(a*c)+(b*c)-2c 则函数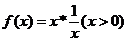 的最小值为 3 .
的最小值为 3 .
14、由抛物线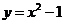 ,直线
,直线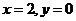 所围成图形的面积是_
所围成图形的面积是_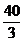 __.
__.
13、命题“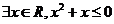 ”的否定是____
”的否定是____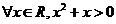 _______.
_______.
12、已知函数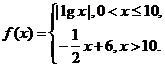 若
若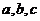 互不相等,且
互不相等,且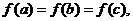 则
则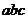 的取值范围是( C )
的取值范围是( C )
A. 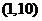 B.
B. 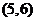 C.
C. 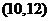 D.
D. 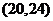
解析: 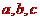 互不相等,不妨设
互不相等,不妨设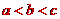
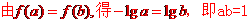
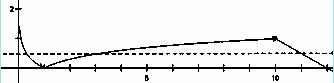
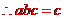 ,显然
,显然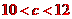
所以选C
命题意图:考察数形结合思想,利用图像处理函数与方程问题
第Ⅱ卷(非选择题共90分)
11、已知函数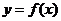 在点
在点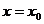 处可导,则
处可导,则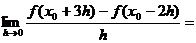 ( D )
( D )
A. 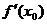 B.
B.
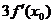 C.
C.
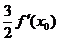 D.
D. 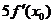
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com