
20.(文)(本小题满分14分)设函数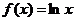 ,
,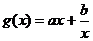 ,函数
,函数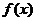 的图象与
的图象与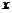 轴的交点也在函数
轴的交点也在函数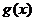 的图象上,且在此点有公切线.
的图象上,且在此点有公切线.
(Ⅰ)求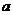 、
、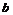 的值;
的值;
(II)证明:当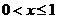 时,
时, 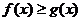 ;当
;当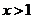 时,
时, 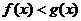 .
.
19.(文)(本小题满分12分)
如图,多面体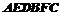 的直观图及三视图如图所示,
的直观图及三视图如图所示,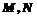 分别为
分别为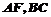 的中点.
的中点.
(Ⅰ)求证: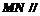 平面
平面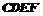 ;
;
(II)求多面体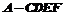 的体积.
的体积.

18. (本小题满分12分) 甲乙二人用4张扑克牌(分别是红桃2, 红桃3, 红桃4, 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(Ⅰ)设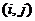 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
(Ⅱ)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜.你认为此游戏是否公平,说明你的理由.
17.(本小题满分12分)
设平面上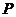 、
、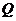 两点的坐标分别是
两点的坐标分别是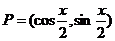 、
、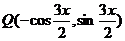 ,其中
,其中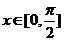 。
。
(Ⅰ)求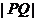 的表达式;
的表达式;
(II)记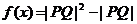 ,求函数
,求函数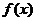 的最小值和最大值。
的最小值和最大值。
16.若一个圆的圆心在抛物线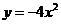 的焦点处,且此圆与直线
的焦点处,且此圆与直线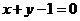 相切,则这个圆的一般方程是_________________。
相切,则这个圆的一般方程是_________________。
15.已知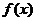 是定义在
是定义在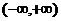 上的减函数,其图象经过
上的减函数,其图象经过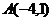 、
、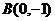 两点,则不等式
两点,则不等式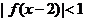 的解集是_________________。
的解集是_________________。
14.若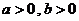 ,且
,且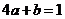 ,则
,则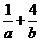 的最小值是 .
的最小值是 .
13.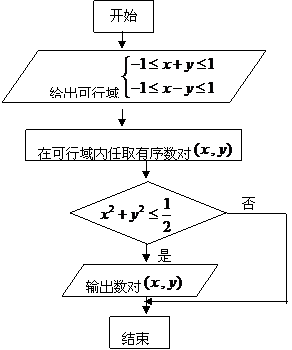 在可行域内任取一点规范如框图所示,则能输出数对
在可行域内任取一点规范如框图所示,则能输出数对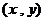 的概率是 .
的概率是 . 













22、(本大题满分14分)
(理)已知函数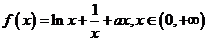 (a为实常数).
(a为实常数).
(Ⅰ)当a = 0时,求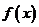 的最小值;
(Ⅱ)若
的最小值;
(Ⅱ)若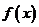 在
在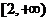 上是单调函数,求a的取值范围;
(Ⅲ)设各项为正的无穷数列
上是单调函数,求a的取值范围;
(Ⅲ)设各项为正的无穷数列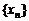 满足
满足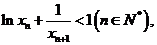
证明: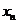 ≤1(n∈N*).
≤1(n∈N*).
(文)设定义在R上的函数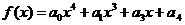
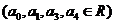 ,当x=-1时,f(x)取极大值
,当x=-1时,f(x)取极大值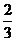 , 且函数y=f(x)的图象关于点(0,0)对称.
, 且函数y=f(x)的图象关于点(0,0)对称.
(Ⅰ)求f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在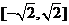 上;
上;
(Ⅲ)设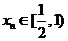
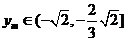 ,求证:
,求证: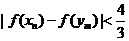 .
.
21、(本大题满分12分)
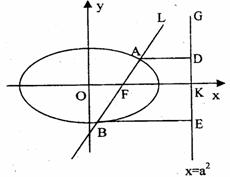
如图,已知直线L: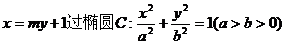 的右焦点F,且交椭圆C于A、B两点,点A、B在直线
的右焦点F,且交椭圆C于A、B两点,点A、B在直线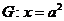 上的射影依次为点D、E。
上的射影依次为点D、E。
(1)若抛物线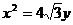 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)(理)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;否则说明理由。
 (文)若
(文)若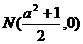 为x轴上一点,求证:
为x轴上一点,求证: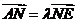
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com