科目：初中数学 来源： 题型：

如图：点E、F分别是菱形ABCD的边BC、CD上的点，且∠EAF=∠D=60°，∠FAD=45°，则∠CFE=

 

度．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

查看答案和解析>>

科目：初中数学 来源：同步题 题型：填空题

如图：点E、F分别是菱形ABCD的边BC、CD上的点且 ∠EAF=∠D=60°，∠FAD=45°，则∠CFE=（     ）。

查看答案和解析>>

科目：初中数学 来源： 题型：

已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．
（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；
（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P． ①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出

1

DM

+

1

DN

的值．

查看答案和解析>>

科目：初中数学 来源：2013-2014学年江苏省江阴市华士片九年级上学期期中考试数学试卷（解析版） 题型：解答题

查看答案和解析>>

科目：初中数学 来源：2013年湖北省黄石市中考数学模拟试卷（解析版） 题型：解答题

已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．
（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；
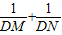（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P． ①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出的值．

查看答案和解析>>

科目：初中数学 来源：2013年湖北省黄石市阳新一中卓越联盟中考数学模拟试卷（解析版） 题型：解答题

已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．
（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；
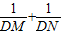（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P． ①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在梯形ABCD中，AD∥BC，若E，F，G，H分别是梯形ABCD各边AB、BC、CD、DA的中点．
（1）求证：四边形EFGH平行四边形；
（2）当梯形ABCD满足什么条件时，四边形EFGH是菱形；
（3）在（2）的条件下，梯形ABCD满足什么条件时，四边形EFGH是正方形．

查看答案和解析>>

科目：初中数学 来源： 题型：

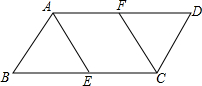如图，在?ABCD中，BC=2AB=4，点E、F分别是BC、AD的中点．
（1）求证：△ABE≌△CDF；
（2）当四边形AECF为菱形时，求出该菱形的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

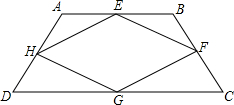
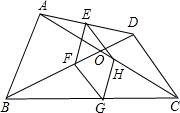如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD、BD、BC、AC的中点．
（1）求证：四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并证明你的结论．

查看答案和解析>>