练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，等边ΔABC中，D为BC上一点, ΔABD经过旋转后到达ΔACE的位置,如果∠BAD=18°,则旋转角等于


    A. 18°
    B.  32°
    C. 60°
    D. 72°
    C
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    8、如图，等边△ABC中，D为BC上一点，△ABD经过旋转后到达△ACE的位置，如果∠BAD=18°，则旋转角等于（　　）

    查看答案和解析>>

    科目：初中数学 来源：第26章《圆》常考题集（02）：26.1 旋转（解析版） 题型：选择题

    如图，等边△ABC中，D为BC上一点，△ABD经过旋转后到达△ACE的位置，如果∠BAD=18°，则旋转角等于（ ）

    A．18°
    B．32°
    C．60°
    D．72°

    查看答案和解析>>

    科目：初中数学 来源：第23章《旋转》常考题集（02）：23.1 图形的旋转（解析版） 题型：选择题

    如图，等边△ABC中，D为BC上一点，△ABD经过旋转后到达△ACE的位置，如果∠BAD=18°，则旋转角等于（ ）

    A．18°
    B．32°
    C．60°
    D．72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，等边△ABC中，D为BC上一点，△ABD经过旋转后到达△ACE的位置，如果∠BAD=18°，则旋转角等于


    1. A.
      18°
    2. B.
      32°
    3. C.
      60°
    4. D.
      72°

    查看答案和解析>>

    科目：初中数学 来源：期中题 题型：单选题

    如图，等边ΔABC中，D为BC上一点, ΔABD经过旋转后到达ΔACE的位置,如果∠BAD=18°,则旋转角等于

    [     ]

    A. 18°
    B.  32°
    C. 60°
    D. 72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

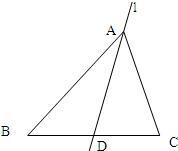    24、如图，已知：AD是△ABC中BC边的中线，则S△ABD=S△ACD，依据是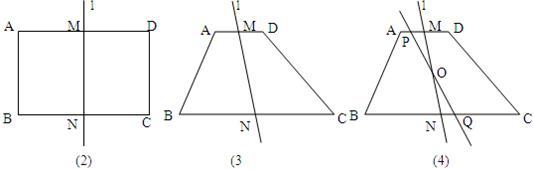
    等底等高的三角形面积相等

    规定；若一条直线l把一个图形分成面积相等的两个图形，则称这样的直线l叫做这个图形的等积直线．根据此定义，在图1中易知直线为△ABC的等积直线．
    （1）如图2，在矩形ABCD中，直线l经过AD，BC边的中点M、N，请你判断直线l是否为该矩形的等积直线
    是
    （填“是”或“否”）．在图2中再画出一条该矩形的等积直线．（不必写作法）
    （2）如图3，在梯形ABCD中，直线l经过上下底AD、BC边的中点M、N，请你判断直线l是否为该梯形的等积直线
    是
    （填“是”或“否”）．
    （3）在图3中，过M、N的中点O任作一条直线PQ分别交AD，BC于点P、Q，如图4所示，猜想PQ是否为该梯形的等积直线？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，△ABC等边三角形，D是BC上一点，△ABD经过旋转后到达△ACE的位置．
    （1）旋转中心是点______；
    （2）旋转角最少是______度；
    （3）如果点M是AB上的一点，那么经过上述旋转后，点M旋转到什么位置？请在图中将点M的对应点M′表示出来；
    （4）如果AM=2，请计算点M旋转到M′过程中所走过的最短的路线长度（结果保留π）；
    （5）如果等边三角形△ABC的边长为6，求四边形ADCE的面积．

    查看答案和解析>>

    科目：初中数学 来源：河北省期中题 题型：探究题

    （1）如图，已知：AD是△ABC中BC边的中线，则S△ABD=S△ACD,依据是                  。
    规定：若一条直线l把一个图形分成面积相等的两个图形，则称这样的直线l叫做这个图形的等积直线。根据此定义，在图1中易知直线为△ABC的等积直线。
    （2）如图2，在矩形ABCD中，直线l经过AD，BC边的中点M. N,请你判断直线l是否为该矩形的等积直线？            （填“是”或“否”）。在图2中再画出一条该矩形的等积直线。（不必写作法）
    （3）如图3，在梯形ABCD中，直线l经过上下底AD. BC边的中点M. N，请你判断直线l是否为该梯形的等积直线？             （填“是”或“否”）。
     （4）在图3中，过M. N的中点O任作一条直线PQ分别交AD，BC于点P. Q,如图4所示，猜想PQ是否为该梯形的等积直线？请说明理由

    查看答案和解析>>

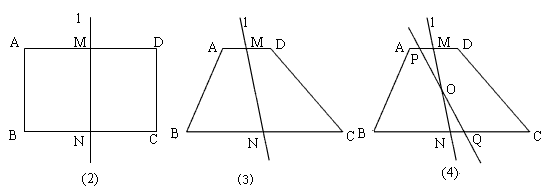
    科目：初中数学 来源： 题型：

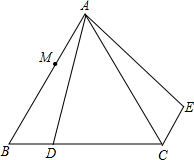    如图，△ABC等边三角形，D是BC上一点，△ABD经过旋转后到达△ACE的位置．
    （1）旋转中心是点
    A
    A
    ；
    （2）旋转角最少是
    60
    60
    度；
    （3）如果点M是AB上的一点，那么经过上述旋转后，点M旋转到什么位置？请在图中将点M的对应点M′表示出来；
    （4）如果AM=2，请计算点M旋转到M′过程中所走过的最短的路线长度（结果保留π）；
    （5）如果等边三角形△ABC的边长为6，求四边形ADCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

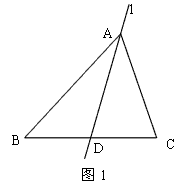
    如图(1)，∆ABC为等边三角形，AB=6，在直角三角板DEF中∠F=90°，∠FDE=60°，点D在边BC上运动，边DF始终经过点A，DE交AC于点G.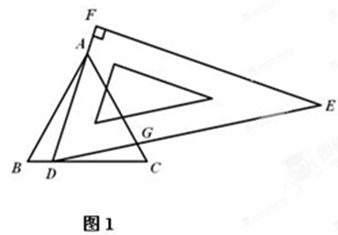

    (1)求证:①∠BAD=∠CDG
    ②∆ABD∽∆DCG
    (2)设BD=x,若CG=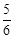，求x的值；
    (3)如图2，当D运动到BC中点时，点P为线段AD上一动点，连接CP，将线段CP绕着点C逆时针旋转60°得到CP' ，连接BP'，DP'，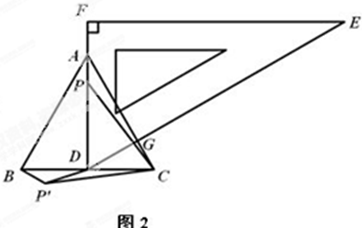

    ①求∠CBP'的度数；②求DP'的最小值.

    查看答案和解析>>


    同步练习册答案