
| 如图, △ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是 |
|
A.  B.AC⊥BD C.四边形ABCD 面积为  D.四边形ABED是等腰梯形 |
科目:初中数学 来源: 题型:
如图, △ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
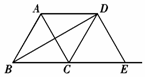
A.![]() B.AC⊥BD
B.AC⊥BD
C.四边形ABCD 面积为![]() D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形
科目:初中数学 来源:福建省中考真题 题型:单选题



科目:初中数学 来源: 题型:
 如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )| A、AD∥BC | ||
| B、AC⊥BD | ||
C、四边形ABCD面积为4
| ||
| D、四边形ABED是等腰梯形 |
科目:初中数学 来源: 题型:
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( ▲ )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为![]() D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形

科目:初中数学 来源: 题型:
 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形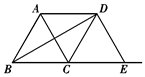
科目:初中数学 来源:2011-2012学年江苏省吴江市九年级5月教学调研测试数学试卷(解析版) 题型:选择题
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形

科目:初中数学 来源:2012年江苏省太仓市毕业暨升学考试模拟数学试卷(解析版) 题型:选择题
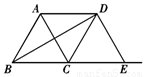
如图,△ABC是边长为2的等边三角形,将△ABC沿射线BC向右平移得到△DCE,连接AD、BD,下列结论错误的是( ▲ )
A.AD∥BC B.AC⊥BD
C.四边形ABCD面积为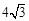 D.四边形ABED是等腰梯形
D.四边形ABED是等腰梯形
科目:初中数学 来源:期中题 题型:解答题
科目:初中数学 来源:2012年山西省中考数学模拟试卷(解析版) 题型:选择题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com