
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
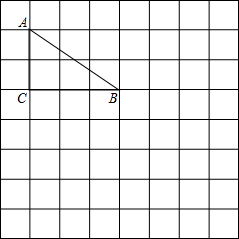 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知直角三角形ABC的三个顶点都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知直角三角形ABC的三个顶点都在格点上.科目:初中数学 来源: 题型:解答题
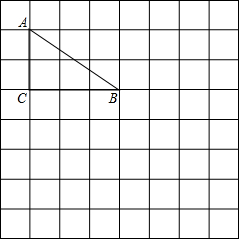 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知直角三角形ABC的三个顶点都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.已知直角三角形ABC的三个顶点都在格点上.科目:初中数学 来源: 题型:
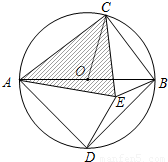
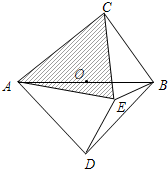
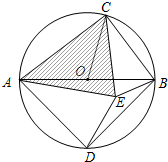 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE.科目:初中数学 来源: 题型:解答题
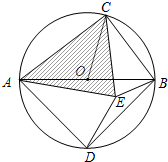 若在⊙O内存在点E,使AE=AD,CB=CE.
若在⊙O内存在点E,使AE=AD,CB=CE.科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(二)(解析版) 题型:解答题
科目:初中数学 来源:期中题 题型:操作题

科目:初中数学 来源:数学教研室 题型:013
下列叙述中,不正确的是
[ ]
A.有公共端点的两条射线组成的图形叫做角
B.角的大小与它的两边的长短无关
C.平角就是两个直角
D.大于90°,小于180°的角叫做钝角
科目:初中数学 来源: 题型:013
下列叙述中,不正确的是
[ ]
A.有公共端点的两条射线组成的图形叫做角
B.角的大小与它的两边的长短无关
C.平角就是两个直角
D.大于90°,小于180°的角叫做钝角
科目:初中数学 来源: 题型:阅读理解
 阅读下面的情景对话,然后解答问题:
阅读下面的情景对话,然后解答问题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com