△ABC三边的长a、b、c都是整数，a＞b＞c，a=8，则满足条件的三角形共有个．

A.
8
B.
9
C.
10
D.
以上都不对

查看答案和解析>>

科目：初中数学 来源：期中题 题型：单选题

⊿ABC三边的长a、b、c都是整数，a＞b＞c，a=8，则满足条件的三角形共有几个

[ ]

A．8
B．9
C．10
D．以上都不对

查看答案和解析>>

科目：初中数学 来源：2010年安徽省中考真题数学试卷 题型：044

如图，已知△ABC∽△A₁B₁C₁，相似比为k(k＞1)，且△ABC的三边长分别为a、b、c(a＞b＞c)，△A₁B₁C₁的三边长分别为a₁、b₁、c₁．

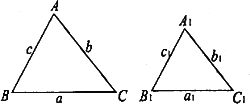
(1)若c＝a₁，求证：a＝kc；

(2)若c＝a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁进都是正整数，并加以说明；

(3)若b＝a₁，c＝b₁，是否存在△ABC和△A₁B₁C₁使得k＝2？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁．
（1）若c=a₁，求证：a=kc；
（2）若c=a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由．

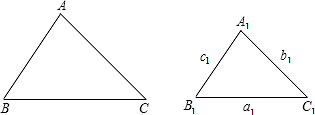
查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁．
（1）若c=a₁，求证：a=kc；
（2）若c=a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由．

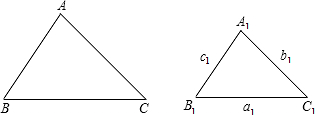
查看答案和解析>>

科目：初中数学 来源：江西省期末题 题型：解答题

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁。
（1）若c=a₁，求证：a=kc；
（2）若c=a1，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由。

查看答案和解析>>

科目：初中数学 来源：2010-2011学年浙江省杭州市滨江区九年级（上）月考数学试卷（11月份）（解析版） 题型：解答题

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁．
（1）若c=a₁，求证：a=kc；
（2）若c=a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由．

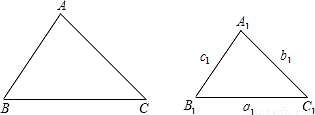
查看答案和解析>>

科目：初中数学 来源：第19章《相似形》中考题集（16）：19.6 相似三角形的性质（解析版） 题型：解答题

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁．
（1）若c=a₁，求证：a=kc；
（2）若c=a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由．

查看答案和解析>>

科目：初中数学 来源：第29章《相似形》中考题集（19）：29.5 相似三角形的性质（解析版） 题型：解答题

如图，已知△ABC∽△A₁B₁C₁，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A₁B₁C₁的三边长分别为a₁、b₁、c₁．
（1）若c=a₁，求证：a=kc；
（2）若c=a₁，试给出符合条件的一对△ABC和△A₁B₁C₁，使得a、b、c和a₁、b₁、c₁都是正整数，并加以说明；
（3）若b=a₁，c=b₁，是否存在△ABC和△A₁B₁C₁使得k=2？请说明理由．

查看答案和解析>>

练习册

高中

初中

小学

△ABC三边的长a、b、c都是整数，a＞b＞c，a=8，则满足条件的三角形共有个．