
| 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形……重复这样的操作,则6次操作后右下角的小正方形面积是 |
|
A.  B.  C.  D.  |
科目:初中数学 来源: 题型:
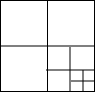 如图,连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2011次操作后右下角的小正方形面积是 ( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2011次操作后右下角的小正方形面积是 ( )科目:初中数学 来源: 题型:
 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:| 5 |
| 5 |
| 5 |
| 5 |
| ||
| 5 |
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源:江苏省连云港市2010年中考一模数学试题 题型:044
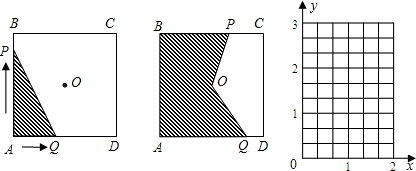
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列问题:

(1)画AD∥BC(D为格点),连接CD;
(2)线段CD的长为________,AC的长为________;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是________;
(4)若E为BC中点,F为AD中点.则tan∠CAE的值是________,四边形AECF的形状为________,面积为________.
科目:初中数学 来源: 题型:
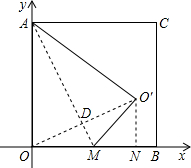 线AM对折,使O点落在O′处,连接OO′,过O′点作O′N⊥OB于N.
线AM对折,使O点落在O′处,连接OO′,过O′点作O′N⊥OB于N.科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
| 2 |
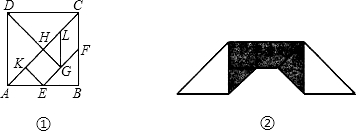
| A、8 | B、6 | C、5 | D、4 |
科目:初中数学 来源: 题型:
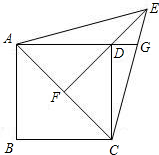 如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连接ED并延长交AC于点F.
如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连接ED并延长交AC于点F.科目:初中数学 来源: 题型:
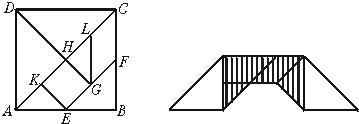
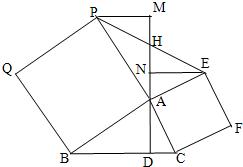 17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.
17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
| BF |
| AF |
| BG |
| AG |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com