
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源:101网校同步练习 初二数学 人教版(新课标2004年初审) 人教版(新课标2004年初审) 题型:013
过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是
A.对角线相等的四边形
B.对角线垂直的四边形
C.对角线互相平分且相等的四边形
D.对角线互相垂直平分的四边形
科目:初中数学 来源: 题型:013
过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是
[ ]
A.对角线相等的四边形
B.对角线垂直的四边形
C.对角线互相平分且相等的四边形
D.对角线互相垂直平分的四边形
科目:初中数学 来源:2012届广东省佛山市南海区九年级上学期期末考试数学试卷(带解析) 题型:解答题
如下图,过四边形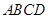 的四个顶点分别作对角线
的四个顶点分别作对角线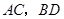 的平行线,所围成的四边形
的平行线,所围成的四边形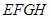 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
小明说:如果一个是平行四边形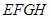 是矩形,则四边形
是矩形,则四边形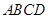 一定是菱形;
一定是菱形;
小亮说:如果一个平行四边形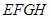 是矩形,则四边形
是矩形,则四边形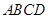 一定是对角线互相垂直的四边形,而不一定是矩形。
一定是对角线互相垂直的四边形,而不一定是矩形。
(1)你认为谁的观点是错误的。
(2)如果四边形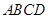 对角线相等,平行四边形
对角线相等,平行四边形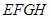 形状为
形状为
(3)如果四边形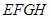 为正方形,则四边形
为正方形,则四边形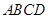 必须满足条件 ,
必须满足条件 ,
并且在下面的网格中画出符合条件(3)的图形并说明理由。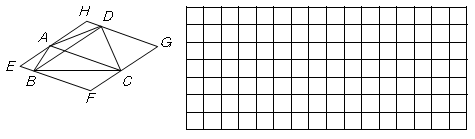
科目:初中数学 来源:2011-2012学年广东省佛山市南海区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如下图,过四边形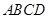 的四个顶点分别作对角线
的四个顶点分别作对角线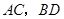 的平行线,所围成的四边形
的平行线,所围成的四边形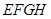 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
小明说:如果一个是平行四边形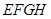 是矩形,则四边形
是矩形,则四边形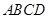 一定是菱形;
一定是菱形;
小亮说:如果一个平行四边形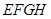 是矩形,则四边形
是矩形,则四边形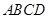 一定是对角线互相垂直的四边形,而不一定是矩形。
一定是对角线互相垂直的四边形,而不一定是矩形。
(1)你认为谁的观点是错误的。
(2)如果四边形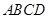 对角线相等,平行四边形
对角线相等,平行四边形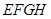 形状为
形状为
(3)如果四边形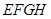 为正方形,则四边形
为正方形,则四边形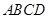 必须满足条件
,
必须满足条件
,
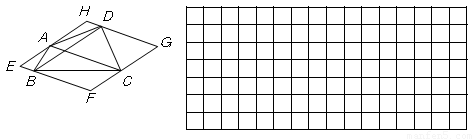
并且在下面的网格中画出符合条件(3)的图形并说明理由。
科目:初中数学 来源:不详 题型:解答题
 的四个顶点分别作对角线
的四个顶点分别作对角线 的平行线,所围成的四边形
的平行线,所围成的四边形 显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧:
显然是平行四边形。在进一步学习时,小明和小亮产生了很大的意见分歧: 是矩形,则四边形
是矩形,则四边形 一定是菱形;
一定是菱形; 是矩形,则四边形
是矩形,则四边形 一定是对角线互相垂直的四边形,而不一定是矩形。
一定是对角线互相垂直的四边形,而不一定是矩形。 对角线相等,平行四边形
对角线相等,平行四边形 形状为
形状为  为正方形,则四边形
为正方形,则四边形 必须满足条件 ,
必须满足条件 ,
科目:初中数学 来源: 题型:
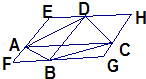 18、如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,如所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是
18、如图,过四边形ABCD的四个顶点分别作对角线AC、BD的平行线,如所围成的四边形EFGH是矩形,则原四边形ABCD需满足的条件是科目:初中数学 来源: 题型:


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com