科目：初中数学 来源： 题型：
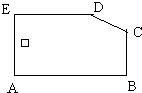18、如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有科目：初中数学 来源： 题型：
科目：初中数学 来源： 题型：
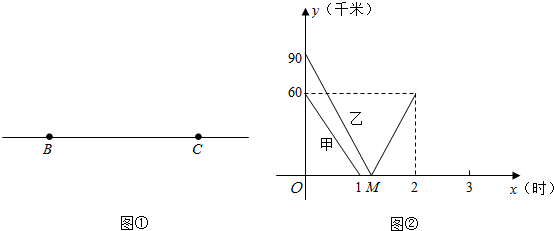
如图①，一条笔直的公路上有A、B、C 三地，B、C 两地相距150千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B 两地．甲、乙两车到A地的距离
、
（千米）与行驶时间x（时）的关系如图②所示． 根据图象②进行以下探究：
1.求图中②M点的坐标，并解释该点的实际意义．
2.在图②中补全甲车的函数图象，求甲车到A地的距离与行驶时间x的函数关系式．
3.A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．
科目：初中数学 来源： 题型：
如图，P为正方形ABCD的对称中心，正方形ABCD的边长为
,
。直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以
个单位每秒速度运动，运动时间为t。求：
1.分别写出A、C、D、P的坐标；
2.当t为何值时，△ANO与△DMR相似？
3.△HCR面积S与t的函数关系式；并求以A、B、C、R为顶点的
四边形是梯形时t的值及S的最大值。
科目：初中数学 来源： 题型：
如图，P为正方形ABCD的对称中心，正方形ABCD的边长为
,
。直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以
个单位每秒速度运动，运动时间为t。求：
1.分别写出A、C、D、P的坐标；
2.当t为何值时，△ANO与△DMR相似？
3.△HCR面积S与t的函数关系式；并求以A、B、C、R为顶点的
四边形是梯形时t的值及S的最大值。
科目：初中数学 来源： 题型：
如图①，一条笔直的公路上有A、B、C 三地，B、C 两地相距150千米，甲、乙两辆汽车分别从
B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B 两地．甲、乙两车到A地的距离
、
（千米）与行驶时间x（时）的关系如图②所示．
根据图象②进行以下探究：
1.求图中②M点的坐标，并解释该点的实际意义．
2.在图②中补全甲车的函数图象，求甲车到A地的距离与行驶时间x的函数关系式．
3.A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．
科目：初中数学 来源： 题型：
,
。直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以
个单位每秒速度运动，运动时间为t。求：
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，点A、O、D以及点B、O、C分别在一条直线上，则圆中弦的条数是（ ）
如图，平面上A．B．C．D．E五个点，其中B．C．D及A．E．C分别在同条一直线上，那么以这5个点中的3个点为顶点的三角形有（ ）