
| 如果边长为2的正方形的两条对角线在两条坐标轴上,对角线交点与坐标原点重合,那么它的四个顶点坐标是 |
A.(1,1)、(-1,1)、(-1,-1)、(1,-1) B.(0,0)、(0,2)、(2,2)、(2,0) C.(  ,0)、(0, ,0)、(0, )、(- )、(- ,0)、(0,- ,0)、(0,- ) )D.(  , , )、(- )、(- ,0)、( ,0)、( ,0)、(0, ,0)、(0, ) ) |
科目:初中数学 来源:不详 题型:单选题
| A.(1,1),(-1,1),(-1,-1),(1,-1) | B.(0,0),(0,2),(2,2)(2,0) | ||||||||||||||||||
C.(
| D.(
|
科目:初中数学 来源: 题型:单选题


科目:初中数学 来源:同步题 题型:单选题
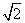 ,0)、(0,
,0)、(0, )、(-
)、(- ,0)、(0,-
,0)、(0,- )
) ,
, )、(-
)、(-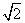 ,0)、(
,0)、( ,0)、(0,
,0)、(0, )
)科目:初中数学 来源:同步轻松练习(七年级数学下) 题型:013
如果边长为2的正方形的两条对角线在两条坐标轴上,对角线交点与坐标原点重合,那么它的四个顶点的坐标是.
A.(1,1)、(-1,1)、(-1,-1)、(1,-1)
B.(0,0)、(0,2)、(2,2)、(2,0)
C.(![]() ,0)、(0,
,0)、(0,![]() )、(-
)、(-![]() ,0)、(0,-
,0)、(0,-![]() )
)
D.(![]() ,
,![]() )、(-
)、(-![]() ,0),(
,0),(![]() ,0)、(0,
,0)、(0,![]() )
)
科目:初中数学 来源: 题型:

科目:初中数学 来源:新课标三维目标导学与测评 数学八年级上册 题型:044
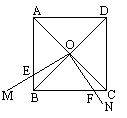
如图,正方形ABCD的边长为a,对角线AC,BD相交于点O,过点O作两条互相垂直的射线OM,ON,组成直角∠MON,当∠MON绕点O旋转时,正方形与∠MON的重叠部分(即四边形BFOE)的面积是否变化,如果变化,说明理由;如果不变化,求出这个面积.
科目:初中数学 来源: 题型:
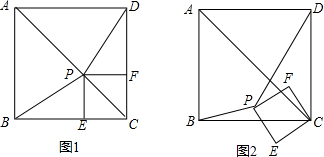
如图所示,长方形是由两个正方形拼成的,正方形的边长为a,对角线为b,长方形对角线为![]() .一只蚂蚁从A点爬形到C点.
.一只蚂蚁从A点爬形到C点.
(1)求蚂蚁爬形的最短路线长(只能按箭头所示的三条路线走),并说明理由.
(2)如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面(实线表示),则蚂蚁从A点到C点的最短路线长是多少?请在图2中画出路线图,若与图中的线段有交点,则要标明并说明交点的准确位置.(可测量猜想判断)
 |
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
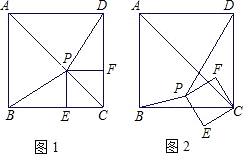 的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com