
如图所示,在△ABC,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知AB=4 , 那么AD=( )。 , 那么AD=( )。 |
|
A.2 B.2  C.4 D.4  |
科目:初中数学 来源: 题型:单选题
如图所示,在△ABC中,∠C=90°,AD是∠BAC的角平分线,且2DC=BD,则∠B满足

科目:初中数学 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:022
如图所示,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,已知AB=![]() ,那么AD=________.
,那么AD=________.

科目:初中数学 来源: 题型:022

科目:初中数学 来源:不详 题型:解答题
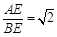 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.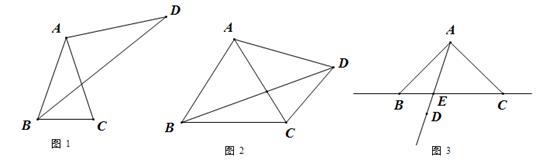
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
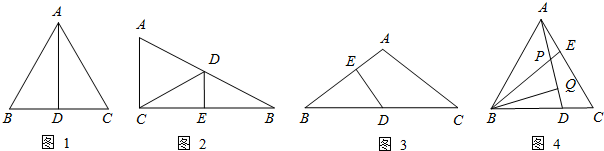
科目:初中数学 来源: 题型:解答题
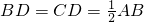 .于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.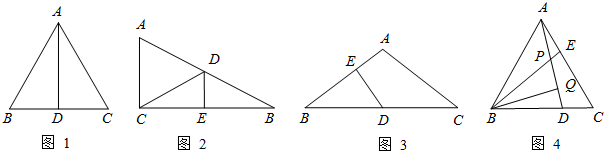
科目:初中数学 来源: 题型:解答题
 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
科目:初中数学 来源:2011-2012学年湖北省武汉市部分学校九年级(上)期末数学试卷(解析版) 题型:解答题
 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com