
| 如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA的角平分线的交点,上述结论中,正确结论的个数是 |
|
A.1个 B.2个 C.3个 D.4个 |
科目:初中数学 来源: 题型:
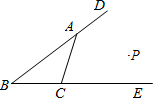 7、如图,已知点P到BE、BD、AC的距离相等,则点P的位置(1)在∠B的平分线上;(2)在∠DAC的平分线上;(3)在∠ECA的平分线上;(4)恰是∠B、∠DAC、∠EAC三条角平分线的交点.上述结论中,正确有
7、如图,已知点P到BE、BD、AC的距离相等,则点P的位置(1)在∠B的平分线上;(2)在∠DAC的平分线上;(3)在∠ECA的平分线上;(4)恰是∠B、∠DAC、∠EAC三条角平分线的交点.上述结论中,正确有科目:初中数学 来源: 题型:解答题
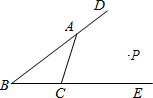 如图,已知点P到BE、BD、AC的距离相等,则点P的位置(1)在∠B的平分线上;(2)在∠DAC的平分线上;(3)在∠ECA的平分线上;(4)恰是∠B、∠DAC、∠ECA三条角平分线的交点.上述结论中,正确有______个.
如图,已知点P到BE、BD、AC的距离相等,则点P的位置(1)在∠B的平分线上;(2)在∠DAC的平分线上;(3)在∠ECA的平分线上;(4)恰是∠B、∠DAC、∠ECA三条角平分线的交点.上述结论中,正确有______个.科目:初中数学 来源:不详 题型:单选题
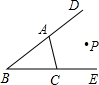
| A.P在∠B的角平分线上 |
| B.P在∠ACE的角平分线上 |
| C.P在∠DAC的角平分线上 |
| D.P到A,B,C三点的距离相等 |
科目:初中数学 来源:《1.4 角平分线》2009年同步练习(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
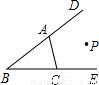
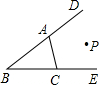 如图,已知点P到BE,BD,AC的距离相等,则下列说法不正确的是
如图,已知点P到BE,BD,AC的距离相等,则下列说法不正确的是科目:初中数学 来源:月考题 题型:单选题

科目:初中数学 来源: 题型:013
如图,已知点P到BE、BD、AC的距离恰好相等,则P点的位置:①在∠B的平分线上,②在∠DAC的平分线上,③在∠ECA的平分线上,④是∠B、∠DAC、∠ECA三条角平分线的交点.其中正确的个数是
[ ]
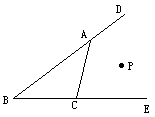
科目:初中数学 来源:湖北省黄冈市蔡河中学2011-2012学年八年级第一次模拟测试数学试题 题型:022
如图已知点P到BE、BD、AC的距离相等,则点P的位置(1)在∠B的平分线上;(2)在∠DAC的平分线上;(3)在∠ECA的平分线上;(4)恰是∠B、∠DAC、∠EAC三条角平分线的交点上述结论中,正确有_________个.

科目:初中数学 来源:三点一测丛书 九年级数学 上 (江苏版课标本) 江苏版课标本 题型:047
阅读下面材料,解答提出的问题.
三角形的三条中线交于一点,这点叫做三角形的重心.三角形的重心与顶点的距离等于它与对边中点距离的两倍.其证明如下:
如图,在△ABC中,P是三条中线AD、BE、CF的交点,求证:PA=2PD.
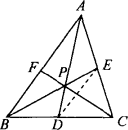
证明:连结DE,∵AE=EC,BD=DC.
∴DE是△ABC的中位线.∴DE∥AB,2DE=AB.
∴![]() =
=![]() =
=![]() .∴PA=2PD.
.∴PA=2PD.
(1)写出上述证明过程中用到的定理或推论;
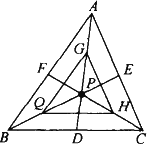
(2)如下图,已知P是△ABC的重心,G、Q分别是AP、BP的中点,QH∥BC交PC于点H,连结GH.求证:AC·PQ=GH·QE.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com