
如图,在△ABC中,设a= ,b= ,b= ,D为线段BC上的点,且|DC|=2|BD|,则 ,D为线段BC上的点,且|DC|=2|BD|,则 等于 等于 |
|
A.  a+ a+ b b B.  a+ a+ b bC.  a- a- b b D.  a- a- b b |
科目:高中数学 来源:0103 期中题 题型:单选题
 ,b=
,b= ,D为线段BC上的点,且|DC|=2|BD|,则
,D为线段BC上的点,且|DC|=2|BD|,则 等于
等于 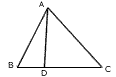
 a+
a+ b
b  a+
a+ b
b a-
a- b
b  a-
a- b
b 科目:高中数学 来源: 题型:解答题
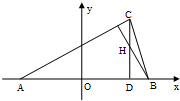 如图,在△ABC中,已知A(-3,0),B(3,0),CD⊥AB于D,△ABC的垂心为
如图,在△ABC中,已知A(-3,0),B(3,0),CD⊥AB于D,△ABC的垂心为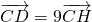 .
.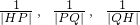 能否成等差数列?请说明理由;
能否成等差数列?请说明理由;科目:高中数学 来源: 题型:解答题
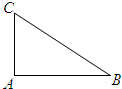 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,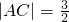 ,一曲线E过点C,且曲线E上任一点到A,B两点的距离之和不变.
,一曲线E过点C,且曲线E上任一点到A,B两点的距离之和不变.科目:高中数学 来源:2010-2011学年湖南省岳阳一中高二(下)数学综合练习试卷7(解析版) 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. 时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;
时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;科目:高中数学 来源:2005-2006学年江苏省常州市武进区前黄高中高二(上)期末数学试卷(解析版) 题型:解答题
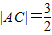 ,一曲线E过点C,且曲线E上任一点到A,B两点的距离之和不变.
,一曲线E过点C,且曲线E上任一点到A,B两点的距离之和不变.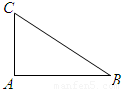
科目:高中数学 来源: 题型:
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
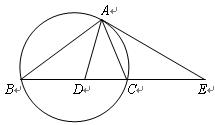
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:![]() 。
。
B.选修4—2 矩阵与变换
在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系![]() 中,点
中,点![]() 是椭圆
是椭圆![]() 上的一个动点,求
上的一个动点,求![]() 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证:![]() 。
。
科目:高中数学 来源:2008年普通高等学校招生全国统一考试数学试题(江苏卷) 题型:解答题
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证: 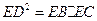 。 。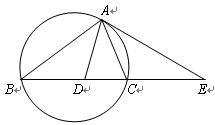 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 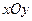 中,设椭圆 中,设椭圆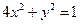 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 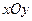 中,点 中,点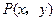 是椭圆 是椭圆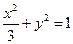 上的一个动点,求 上的一个动点,求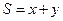 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
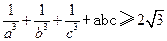 。
。科目:高中数学 来源:2012年人教A版高中数学必修二空间点、直线、平面之间的位置关系练习卷(二) 题型:解答题
如图,正三角形ABC的边长为2,D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠,使A、B、C三点重合,构成三棱锥A— DEF .

(I)求平面ADE与底面DEF所成二面角的余弦值
(Ⅱ)设点M、N分别在AD、EF上, (λ>O,λ为变量)
(λ>O,λ为变量)
①当λ为何值时,MN为异面直线AD与EF的公垂线段? 请证明你的结论②设异面直线MN与AE所成的角为a,异面直线MN与DF所成的角为β,试求a+β 的值
科目:高中数学 来源:2008年普通高等学校招生全国统一考试数学试题(江苏卷) 题型:解答题
从A,B,C,D四个中选做2个,每题10分,共20分
A.选修4—1 几何证明选讲
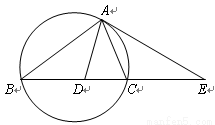
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证: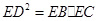 。
。
B.选修4—2 矩阵与变换
在平面直角坐标系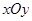 中,设椭圆
中,设椭圆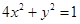 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。
C.选修4—4 参数方程与极坐标
在平面直角坐标系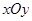 中,点
中,点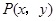 是椭圆
是椭圆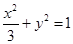 上的一个动点,求
上的一个动点,求 的最大值。
的最大值。
D.选修4—5 不等式证明选讲
设a,b,c为正实数,求证: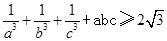 。
。
科目:高中数学 来源:不详 题型:解答题
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。 |
| B.选修4—2 矩阵与变换 在平面直角坐标系  中,设椭圆 中,设椭圆 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系  中,点 中,点 是椭圆 是椭圆 上的一个动点,求 上的一个动点,求 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
 。
。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com