
用数学归纳法证明等式: 的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到 的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到 |
A.1+3+5+…+(2k+1)=k2 B.1+3+5+…+(2k+1)=(k+1)2 C.1+3+5+…+(2k+1)=(k+2)2 D.1+3+5+…+(2k+1)=(k+3)2 |
科目:高中数学 来源:吉林省期中题 题型:单选题
 的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到
的过程中,第二步假设n=k时等式成立,则当n=k+1时应得到科目:高中数学 来源:2010年安徽省高考数学最后冲刺试卷(六)(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:成都一模 题型:单选题
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
A.
| B.
| ||||||||||
C.
| D.
|
科目:高中数学 来源:2011-2012学年湖北省荆州二中高三(上)期末数学试卷(理科)(解析版) 题型:选择题
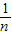 +
+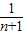 +…+
+…+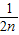 <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )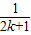 +
+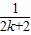
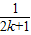 +
+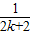 -
-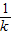
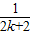 -
-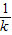
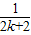 -
-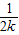
科目:高中数学 来源:2012年四川省成都市高考数学一模试卷(理科)(解析版) 题型:选择题
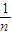 +
+ +…+
+…+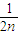 <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( )
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=( ) +
+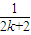
 +
+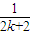 -
-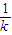
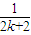 -
-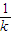
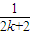 -
-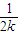
科目:高中数学 来源: 题型:单选题
 +
+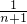 +…+
+…+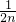 <1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=
<1(n∈N*,n≥3)的过程中:假设当n=k(k∈N*,k≥3)时,不等式f(k)<1成立,则需证当n=k+1时,f(k+1)<1也成立.若f(k+1)=f(k)+g(k),则g(k)=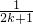 +
+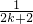
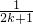 +
+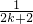 -
-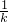
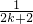 -
-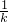
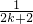 -
-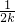
科目:高中数学 来源: 题型:
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
科目:高中数学 来源:山西大学附中2009届高三12月月考试题(理) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com