练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设数集，，P={x|0≤x≤1}，且M，N都是集合P的子集，如果把b-a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是

    A.
    B.
    C.
    D.
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：泉州模拟 题型：填空题

    设集合P⊆Z，且满足下列条件：
    （1）?x，y∈P，x+y∈P；       
    （2）-1∉P；
    （3）P中的元素有正数，也有负数； 
    （4）P中存在是奇数的元素．
    现给出如下论断：
    ①P可能是有限集；
    ②?m，n∈P，mn∈P；
    ③0∈P；         
    ④2∉P．
    其中正确的论断是______． （写出所有正确论断的序号）

    查看答案和解析>>

    科目：高中数学 来源：2013年福建省泉州市高三5月质检数学试卷（理科）（解析版） 题型：填空题

    设集合P⊆Z，且满足下列条件：
    （1）?x，y∈P，x+y∈P；       
    （2）-1∉P；
    （3）P中的元素有正数，也有负数； 
    （4）P中存在是奇数的元素．
    现给出如下论断：
    ①P可能是有限集；
    ②?m，n∈P，mn∈P；
    ③0∈P；         
    ④2∉P．
    其中正确的论断是    ． （写出所有正确论断的序号）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏五校高三下学期期初教学质量调研数学卷（解析版） 题型：解答题

    设函数f (x)的定义域为M，具有性质P：对任意x∈M，都有f (x)＋f (x＋2)≤2f (x＋1).

    （1）若M为实数集R，是否存在函数f (x)＝ax (a＞0且a≠1，x∈R) 具有性质P，并说明理由；

    （2）若M为自然数集N，并满足对任意x∈M，都有f (x)∈N. 记d(x)＝f (x＋1)－f (x).

    (ⅰ) 求证：对任意x∈M，都有d(x＋1)≤d(x)且d(x)≥0；

    (ⅱ) 求证：存在整数0≤c≤d(1)及无穷多个正整数n，满足d(n)＝c.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数f (x)的定义域为M，具有性质P：对任意x∈M，都有f (x)＋f (x＋2)≤2f (x＋1).
    （1）若M为实数集R，是否存在函数f (x)＝ax (a＞0且a≠1，x∈R) 具有性质P，并说明理由；
    （2）若M为自然数集N，并满足对任意x∈M，都有f (x)∈N. 记d(x)＝f (x＋1)－f (x).
    (ⅰ) 求证：对任意x∈M，都有d(x＋1)≤d(x)且d(x)≥0；
    (ⅱ) 求证：存在整数0≤c≤d(1)及无穷多个正整数n，满足d(n)＝c.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设函数f (x)的定义域为M，具有性质P：对任意x∈M，都有f (x)＋f (x＋2)≤2f (x＋1).
    （1）若M为实数集R，是否存在函数f (x)＝ax (a＞0且a≠1，x∈R) 具有性质P，并说明理由；
    （2）若M为自然数集N，并满足对任意x∈M，都有f (x)∈N. 记d(x)＝f (x＋1)－f (x).
    (ⅰ) 求证：对任意x∈M，都有d(x＋1)≤d(x)且d(x)≥0；
    (ⅱ) 求证：存在整数0≤c≤d(1)及无穷多个正整数n，满足d(n)＝c.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•泉州模拟）设集合P⊆Z，且满足下列条件：
    （1）?x，y∈P，x+y∈P；       
    （2）-1∉P；
    （3）P中的元素有正数，也有负数； 
    （4）P中存在是奇数的元素．
    现给出如下论断：
    ①P可能是有限集；
    ②?m，n∈P，mn∈P；
    ③0∈P；         
    ④2∉P．
    其中正确的论断是
    ①Ⅱ②③④
    ①Ⅱ②③④
    ． （写出所有正确论断的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合Sn={X|X=（x1，x2，…，xn），xi∈{0，1}，i=1，2，…，n}（n≥2）对于A=（a1，a2，…an，），B=（b1，b2，…bn，）∈Sn，定义A与B的差为A-B=（|a1-b1|，|a2-b2|，…|an-bn|）；
    A与B之间的距离为d(A，B)=
    n
    i=1
    |ai-bi|
    （Ⅰ）证明：?A，B，C∈Sn，有A-B∈Sn，且d（A-C，B-C）=d（A，B）；
    （Ⅱ）证明：?A，B，C∈Sn，d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数
    （Ⅲ）设P⊆Sn，P中有m（m≥2）个元素，记P中所有两元素间距离的平均值为
    .
    d
    (P)    ．
    证明：
    .
    d
    (P)    ≤
    mn
    2(m-1)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系中，已知O为坐标原点，点A的坐标为（a，b），点B的坐标为（cosωx，sinωx），其中a2+b2≠0且ω＞0．设f(x)=
    OA
    •
    OB
    ．
    （1）若a=
    		3
    ，b=1，ω=2，求方程f（x）=1在区间[0，2π]内的解集；
    （2）若点A是过点（-1，1）且法向量为
    n
    =(-1，1)    的直线l上的动点．当x∈R时，设函数f（x）的值域为集合M，不等式x2+mx＜0的解集为集合P．若P⊆M恒成立，求实数m的最大值；
    （3）根据本题条件我们可以知道，函数f（x）的性质取决于变量a、b和ω的值．当x∈R时，试写出一个条件，使得函数f（x）满足“图象关于点(
    π
    3
    ，0)    对称，且在x=
    π
    6
    处f（x）取得最小值”．

    查看答案和解析>>

    科目：高中数学 来源：0113 期中题 题型：单选题

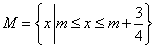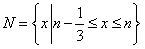    设数集，，P={x|0≤x≤1}，且M，N都是集合P的子集，如果把b-a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是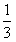
    [     ]
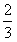
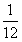
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州十四中2011－2012学年高一上学期期中考试数学试题 题型：013

    设数集，，P＝{x|0≤x≤1}，且M，N都是集合P的子集，如果把b－a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>


    同步练习册答案