练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数图象的对称轴方程可以为

    A、x=
    B、x=
    C、x=
    D、x=
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：北京期末题 题型：单选题

    函数图象的对称轴方程可以为
    [     ]
    A、x=
    B、x=
    C、x=
    D、x=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    当函数的自变量取值区间与值域区间相同时，我们称这样的区间为该函数的保值区间．函数的保值区间有（-∞，m]、[m，n]、[n，+∞）三种形式．以下四个图中：虚线为二次函数图象的对称轴，直线l的方程为y=x，从图象可知，下列四个二次函数中有2个保值区间的函数是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省江门市鹤山一中高三（上）期中数学试卷（文科）（解析版） 题型：选择题

    当函数的自变量取值区间与值域区间相同时，我们称这样的区间为该函数的保值区间．函数的保值区间有（-∞，m]、[m，n]、[n，+∞）三种形式．以下四个图中：虚线为二次函数图象的对称轴，直线l的方程为y=x，从图象可知，下列四个二次函数中有2个保值区间的函数是（ ）
    A．
    B．
    C．
    D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    当函数的自变量取值区间与值域区间相同时，我们称这样的区间为该函数的保值区间．函数的保值区间有（-∞，m]、[m，n]、[n，+∞）三种形式．以下四个图中：虚线为二次函数图象的对称轴，直线l的方程为y=x，从图象可知，下列四个二次函数中有2个保值区间的函数是


    1. A.
    2. B.
    3. C.
    4. D.

    查看答案和解析>>

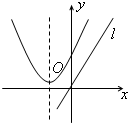
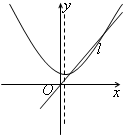
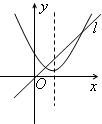
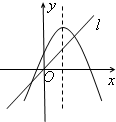
    科目：高中数学 来源：黑龙江省哈三中2011－2012学年高一上学期期中考试数学试题 题型：013

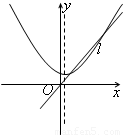
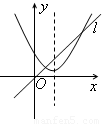
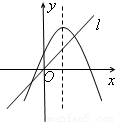
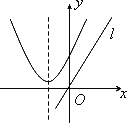
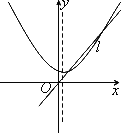
    当函数的自变量取值区间与值域区间相同时，我们称这样的区间为该函数的保值区间．函数的保值区间有(－∞，m]、[m，n]、[n，＋∞)三种形式．以下四个图中：虚线为二次函数图像的对称轴，直线l的方程为y＝x，从图象可知，下列四个二次函数中有2个保值区间的函数是

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

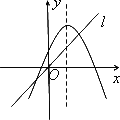
    科目：高中数学 来源： 题型：解答题

    已知函数f（x）=Asinωx+Bcosωx（其中A、B、ω是非零常数，且ω＞0）的最小正周期为2，且当x=数学公式时，f（x）取得最大值2．
    （1）求函数f（x）的表达式；
    （2）求函数f（x+数学公式）的单调递增区间，并指出该函数的图象可以由函数y=2sinx，x∈R的图象经过怎样的变换得到？
    （3）在闭区间[数学公式]上是否存在f（x）的对称轴？如果存在，求出其对称轴方程；如果不存在，则说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=Asinωx+Bcosωx（其中A、B、ω是非零常数，且ω＞0）的最小正周期为2，且当x=
    1
    3
    时，f（x）取得最大值2．
    （1）求函数f（x）的表达式；
    （2）求函数f（x+
    1
    6
    ）的单调递增区间，并指出该函数的图象可以由函数y=2sinx，x∈R的图象经过怎样的变换得到？
    （3）在闭区间[
    21
    4
    ，
    23
    4
    ]上是否存在f（x）的对称轴？如果存在，求出其对称轴方程；如果不存在，则说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数f（x）=Asinωx+Bcosωx（其中A、B、ω是非零常数，且ω＞0）的最小正周期为2，且当x=
    1
    3
    时，f（x）取得最大值2．
    （1）求函数f（x）的表达式；
    （2）求函数f（x+
    1
    6
    ）的单调递增区间，并指出该函数的图象可以由函数y=2sinx，x∈R的图象经过怎样的变换得到？
    （3）在闭区间[
    21
    4
    ，
    23
    4
    ]上是否存在f（x）的对称轴？如果存在，求出其对称轴方程；如果不存在，则说明理由．

    查看答案和解析>>


    同步练习册答案