| 在数列{an}中,已知S1=1,S2=2,且Sn+1-3Sn+2Sn-1=0(n∈N*),则此数列 |
A.为等差数列
B.为等比数列
C.从第二项起为等差数列
D.从第二项起为等比数列 |
相关习题
科目:高中数学
来源:月考题
题型:单选题
在数列{an}中,已知S1=1,S2=2,且Sn+1-3Sn+2Sn-1=0(n∈N*),则此数列
A.为等差数列
B.为等比数列
C.从第二项起为等差数列
D.从第二项起为等比数列
查看答案和解析>>
科目:高中数学
来源:
题型:
已知数列{a
n}中,a
1=1,且点P(a
n,a
n+1)(n∈N
*)在直线x-y+1=0上.
(1)求数列{a
n}的通项公式;
(2)若函数
f(n)=+++…+(n∈N,且n≥2),求函数f(n)的最小值;
(3)设
bn=,Sn表示数列{b
n}的前项和.试问:是否存在关于n的整式g(n),使得S
1+S
2+S
3+…+S
n-1=(S
n-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学
来源:0110 期中题
题型:解答题
已知数列{an}中,a1=1,且点P(an,an+1)(n∈N*)在直线x-y+1=0上。
(1)求数列{an}的通项公式;
(2)若函数 (n∈N,且n≥2),求函数f(n)的最小值;
(n∈N,且n≥2),求函数f(n)的最小值;
(3)设bn=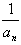 ,Sn表示数列{bn}的前n项和。试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立? 若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由。
,Sn表示数列{bn}的前n项和。试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立? 若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由。
查看答案和解析>>
科目:高中数学
来源:2009-2010学年福建省福州三中高二(上)期中数学试卷(文科)(解析版)
题型:解答题
已知数列{a
n}中,a
1=1,且点P(a
n,a
n+1)(n∈N
*)在直线x-y+1=0上.
(1)求数列{a
n}的通项公式;
(2)设

,求数列{b
n}的前n项和T
n;
(3)设

表示数列{b
n}的前n项和.试问:是否存在关于n的整式g(n),使得S
1+S
2+S
3+…+S
n-1=(S
n-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年福建省福州三中高二(上)期中数学试卷(理科)(解析版)
题型:解答题
已知数列{a
n}中,a
1=1,且点P(a
n,a
n+1)(n∈N
*)在直线x-y+1=0上.
(1)求数列{a
n}的通项公式;
(2)设

,求数列{b
n}的前n项和T
n;
(3)设

表示数列{b
n}的前n项和.试问:是否存在关于n的整式g(n),使得S
1+S
2+S
3+…+S
n-1=(S
n-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2011•徐州模拟)已知各项均为正数的等比数列{a
n}的公比为q,且0<q<
.
(1)在数列{a
n}中是否存在三项,使其成等差数列?说明理由;
(2)若a
1=1,且对任意正整数k,a
k-(a
K+1+a
k+2)仍是该数列中的某一项.
(ⅰ)求公比q;
(ⅱ)若b
n=-log
an+1(
+1),S
n=b
1+b
2+…+b
n,T
n=S
1+S
2+…+S
n,试用S
2011 表示T
2011.
查看答案和解析>>
科目:高中数学
来源:同升湖国际实验学校2007届高三第三次模拟考试数学试卷(文)
题型:044
|
|
解答题:解答应写出文字说明,证明过程或演算步骤.
已知数列{an}中,a1=1且点P(an,an+1)(n∈N*)在直线x-y+1=0上.
| (1) |
|
(2) |
|
若函数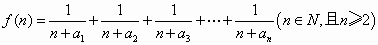
求证:f(n)≥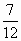
|
|
(3) |
|
设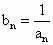 ,Sn表示数列{bn}的前项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立?若不存在,试说明理由.若存在,写出g(n)的解析式,并加以证明 ,Sn表示数列{bn}的前项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立?若不存在,试说明理由.若存在,写出g(n)的解析式,并加以证明
|
|
|
查看答案和解析>>
科目:高中数学
来源:
题型:
(2009•连云港二模)已知函数f(x)=kx+m,当x∈[a1,b1]时,f(x)的值域为[a2,b2],当x∈[a2,b2]时,f(x)的值域为[a3,b3],依此类推,一般地,当x∈[an-1,bn-1]时,f(x)的值域为[an,bn],其中k、m为常数,且a1=0,b1=1.
(1)若k=1,求数列{an},{bn}的通项公式;
(2)若k>0且k≠1,问是否存在常数m,使数列{bn}是公比不为1的等比数列?请说明理由;
(3)若k<0,设数列{an},{bn}的前n项和分别为Sn,Tn,求(T1+T2+…+T2008)-(S1+S2+…+S2008).
查看答案和解析>>
科目:高中数学
来源:山西省实验中学2006-2007学年度第一学期高三年级第三次月考 数学试题
题型:044
|
|
解答题:解答应写出文字说明,证明过程或演算步骤
已知数列{an}中a1=1,且P(an,an+1)在直线x-y+1=0上,
| (1) |
|
(2) |
|
若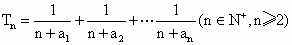 ,求Tn的最小值 ,求Tn的最小值
|
|
(3) |
|
若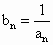 ,Sn是{bn}的前n项和,问:是否存在关于n的整式g(n)使得S1+S2+…+Sn-1=(Sn-1)g(n)对一切n≥2的自然n恒成立说明理由. ,Sn是{bn}的前n项和,问:是否存在关于n的整式g(n)使得S1+S2+…+Sn-1=(Sn-1)g(n)对一切n≥2的自然n恒成立说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:上海模拟题
题型:解答题
已知函数f(x)=kx+m,当x∈[a
1,b
1]时,f(x)的值域为[a
2,b
2],当x∈[a
2,b
2]时,f(x)的值域为[a
3,b
3],依次类推,一般地,当x∈[a
n-1,b
n-1]时,f(x)的值域为[a
n,b
n],其中k,m为常数,且a
1=0,b
1=1,
(Ⅰ)若k=1,求数列{a
n},{b
n}的通项公式;
(Ⅱ)若m=2,问是否存在常数k>0,使得数列{b
n}满足

?若存在,求k的值;若不存在,请说明理由;
( Ⅲ)若k<0,设数列{a
n},{b
n}的前n项和分别为S
n,T
n,求(T
1+T
2+…+ T
2010)-(S
1+S
2+…+S
2010)。
查看答案和解析>>

 (n∈N,且n≥2),求函数f(n)的最小值;
(n∈N,且n≥2),求函数f(n)的最小值;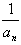 ,Sn表示数列{bn}的前n项和。试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立? 若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由。
,Sn表示数列{bn}的前n项和。试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)·g(n)对于一切不小于2的自然数n恒成立? 若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由。  ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; 表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由. ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; 表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
表示数列{bn}的前n项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由. ?若存在,求k的值;若不存在,请说明理由;
?若存在,求k的值;若不存在,请说明理由;