| 设数列{an}是首项为1,公比为3的等比数列,把{an}中每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N+,下列结论正确的是 |
A.bn+1=3bn且Sn= (3n-1) (3n-1)
B.bn+1=3bn-2且Sn= (3n-1) (3n-1)
C.bn+1=3bn+4且Sn= (3n-1)-2n (3n-1)-2n
D.bn+1=3bn-4且Sn= (3n-1)-2n (3n-1)-2n |
相关习题
科目:高中数学
来源:河南省模拟题
题型:单选题
设数列{an}是首项为1,公比为3的等比数列,把{an}中每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N+,下列结论正确的是
A.b
n+1=3b
n且S
n=
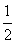
(3
n-1)
B.b
n+1=3b
n-2且S
n=

(3
n-1)
C.b
n+1=3b
n+4且S
n=
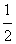
(3
n-1)-2n
D.b
n+1=3b
n-4且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:模拟题
题型:单选题
设数列{an}是首项为1、公比为3的等比数列,把{an}中的每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N*,下列结论正确的是
A、b
n+1=3b
n,且S
n=
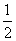
(3
n-1)
B、b
n+1=3b
n-2,且S
n=

(3
n-1)
C、b
n+1=3b
n+4,且S
n=
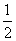
(3
n-1)-2n
D、b
n+1=3b
n-4,且S
n=
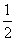
(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:
题型:
设数列{an}是首项为1,公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn},设An、Bn分别是数列{an}和{bn}的前n项和.
(1)a10是数列{bn}的第几项;
(2)是否存在正整数m,使Bm=2010?若不存在,请说明理由;否则,求出m的值;
(3)设am是数列{bn}的第f(m)项,试比较:Bf(m)与2Am的大小,请详细论证你的结论.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
设数列{an}是首项为1,公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn},设An、Bn分别是数列{an}和{bn}的前n项和.
(1)a10是数列{bn}的第几项;
(2)是否存在正整数m,使Bm=2010?若不存在,请说明理由;否则,求出m的值;
(3)设am是数列{bn}的第f(m)项,试比较:Bf(m)与2Am的大小,请详细论证你的结论.
查看答案和解析>>
科目:高中数学
来源:吉安二模
题型:解答题
设数列{an}是首项为1,公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn},设An、Bn分别是数列{an}和{bn}的前n项和.
(1)a10是数列{bn}的第几项;
(2)是否存在正整数m,使Bm=2010?若不存在,请说明理由;否则,求出m的值;
(3)设am是数列{bn}的第f(m)项,试比较:Bf(m)与2Am的大小,请详细论证你的结论.
查看答案和解析>>
科目:高中数学
来源:2007-2008学年湖北省武汉市华中师大一附中高三(上)期中数学试卷(理科)(解析版)
题型:解答题
设数列{an}是首项为1,公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn},设An、Bn分别是数列{an}和{bn}的前n项和.
(1)a10是数列{bn}的第几项;
(2)是否存在正整数m,使Bm=2010?若不存在,请说明理由;否则,求出m的值;
(3)设am是数列{bn}的第f(m)项,试比较:Bf(m)与2Am的大小,请详细论证你的结论.
查看答案和解析>>
科目:高中数学
来源:2010年江西省吉安市高考数学二模试卷(理科)(解析版)
题型:解答题
设数列{an}是首项为1,公差为2的等差数列,对每一个k∈N*,在ak与ak+1之间插入2k-1个2,得到新数列{bn},设An、Bn分别是数列{an}和{bn}的前n项和.
(1)a10是数列{bn}的第几项;
(2)是否存在正整数m,使Bm=2010?若不存在,请说明理由;否则,求出m的值;
(3)设am是数列{bn}的第f(m)项,试比较:Bf(m)与2Am的大小,请详细论证你的结论.
查看答案和解析>>
科目:高中数学
来源:2010年安徽省高考数学冲刺试卷(文科)(解析版)
题型:选择题
设数列{a
n}是首项为1公比为3的等比数列,把{a
n}中的每一项都减去2后,得到一个新数列{b
n},{b
n}的前n项和为S
n,对任意的n∈N
*,下列结论正确的是( )
A.b
n+1=3b
n,且S
n=

(3
n-1)
B.b
n+1=3b
n-2,且S
n=

(3
n-1)
C.b
n+1=3b
n+4,且S
n=

(3
n-1)-2n
D.b
n+1=3b
n-4,且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:2011年高考数学复习:5.4 数列求和(解析版)
题型:选择题
设数列{a
n}是首项为1公比为3的等比数列,把{a
n}中的每一项都减去2后,得到一个新数列{b
n},{b
n}的前n项和为S
n,对任意的n∈N
*,下列结论正确的是( )
A.b
n+1=3b
n,且S
n=

(3
n-1)
B.b
n+1=3b
n-2,且S
n=

(3
n-1)
C.b
n+1=3b
n+4,且S
n=

(3
n-1)-2n
D.b
n+1=3b
n-4,且S
n=

(3
n-1)-2n
查看答案和解析>>
科目:高中数学
来源:
题型:
已知{an}是首项为19,公差为-2的等差数列,sn为{an}的前n项和.
(1)求通项an及sn;
(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及其前n项和Tn.
查看答案和解析>>

 (3n-1)
(3n-1) (3n-1)
(3n-1) (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n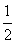 (3n-1)
(3n-1) (3n-1)
(3n-1)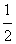 (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n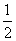 (3n-1)
(3n-1) (3n-1)
(3n-1)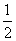 (3n-1)-2n
(3n-1)-2n 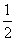 (3n-1)-2n
(3n-1)-2n  (3n-1)
(3n-1) (3n-1)
(3n-1) (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n (3n-1)
(3n-1) (3n-1)
(3n-1) (3n-1)-2n
(3n-1)-2n (3n-1)-2n
(3n-1)-2n