设椭圆 （a＞b＞0）的离心率 ，右焦点F（c，0），方程ax2+bx-c=0的两根分别为x1、x2，则点P（x1，x2）在 |
A.圆x2+y2=2内 B.圆x2+y2=2上 C.圆x2+y2=2外 D.以上三种情况都有可能 |
科目：高中数学 来源：2010-2011学年浙江省宁波市鄞州高级中学高二（上）10月月考数学试卷（解析版） 题型：选择题
（a＞b＞0）的离心率e=
，右焦点为F（c，0），方程ax2+bx+c=0的两个实数根分别为x1和x2，则点P（x1，x2）必在（ ）科目：高中数学 来源：2010-2011学年浙江省温州市龙湾中学高二（下）期末数学试卷（理科）（解析版） 题型：选择题
（a＞b＞0）的离心率e=
，右焦点为F（c，0），方程ax2+bx+c=0的两个实数根分别为x1和x2，则点P（x1，x2）必在（ ）科目：高中数学 来源：2010年浙江省舟山市七校高三第二次质量调研数学试卷（理科）（解析版） 题型：选择题
（a＞b＞0）的离心率
，A、B是椭圆上关于x、y轴均不对称的两点，线段AB的垂直平分线与x轴交于点P（1，0），设AB的中点为C（x，y），则x的值为（ ）
科目：高中数学 来源： 题型：单选题
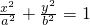（a＞b＞0）的离心率
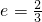，A、B是椭圆上关于x、y轴均不对称的两点，线段AB的垂直平分线与x轴交于点P（1，0），设AB的中点为C（x0，y0），则x0的值为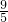
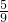
科目：高中数学 来源： 题型：单选题
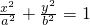（a＞b＞0）的离心率e=
，右焦点为F（c，0），方程ax2+bx+c=0的两个实数根分别为x1和x2，则点P（x1，x2）必在科目：高中数学 来源：2011-2012学年安徽省黄山市高三第二次质量检测数学试卷（理科）（解析版） 题型：解答题
（a＞b＞0）的离心率
，A、B分别为椭圆长轴右端点与短轴上端点，坐标原点O到直线AB的距离为
．
，记
，求证：（6f（λ）-32）k2=-3f（λ）；科目：高中数学 来源： 题型：解答题
已知椭圆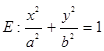
（a＞b＞0）的离心率为
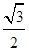，且过点（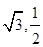
）．
（1）求椭圆E的方程；
（2）设直线l:y=kx+t与圆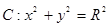
（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.
①求证：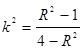
；
②当R为何值时，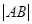
取得最大值？并求出最大值．
科目：高中数学 来源： 题型：解答题
已知椭圆
（a＞b＞0）的离心率为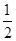
，以原点为圆心，椭圆短半轴长半径的圆与直线y=x+
相切.
(1)求椭圆的方程；
(2)设直线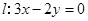
与椭圆在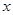
轴上方的一个交点为
，
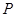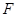是椭圆的右焦点，试探究以
为
直径的圆与以椭圆长轴为直径的圆的位置关系.
科目：高中数学 来源：不详 题型：解答题
（a＞b＞0）的离心率为
，且过点（
）．
（1＜R＜2）相切于点A，且l与椭圆E只有一个公共点B.
；
取得最大值？并求出最大值．科目：高中数学 来源： 题型：解答题
设椭圆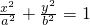（a＞b＞0）的两个焦点是F1（-c，0），F2（c，0）（c＞0），且椭圆上存在点P使得直线PF1与直线PF2垂直．
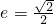，且△PQF2的面积为12时，求椭圆方程．湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com