| 已知抛物线y2=4x上两个动点B、C和点A（1，2），且∠BAC=90°，则动直线BC必过定点 |
A.（2，5） B.（-2，5） C.（5，-2） D.（5，2） |
科目：高中数学 来源：同步题 题型：单选题
科目：高中数学 来源： 题型：
(1)点P在椭圆C1的短轴的一个端点B与焦点F的连线上，且
，求点P的轨迹C2的方程；
(2)若直线x+y+m=0与点P的轨迹C2交于两点M、N，问是否存在实数m，使OM⊥ON成立.若存在，求出m的值，若不存在，说明理由.
科目：高中数学 来源： 题型：
(1)点P在椭圆C1的短轴的一个端点B与焦点F的连线上，且
，求点P的轨迹C2的方程；
(2)若直线x+y+m=0与点P的轨迹C2交于两点M、N，问是否存在实数m，使OM⊥ON成立.若存在，求出m的值，若不存在，说明理由.
科目：高中数学 来源：101网校同步练习 高二数学 苏教版(新课标·2004年初审) 苏教版 题型：044
已知抛物线C：y2＝4x，F为其焦点，
(1)若过焦点F且斜率为1的直线与抛物线C交于A、B两点，求弦AB的长；
(2)若过点M(2，1)的一条直线交抛物线C于P、Q两点，且PQ被M平分，求这条直线的方程；
(3)设点R、S是抛物线C上原点O以外的两个动点，且OR⊥OS，若作ON⊥RS，垂足为N，求点N的轨迹方程，并说明它表示什么曲线．
科目：高中数学 来源：2008年高考数学模拟创新试题分类汇编(解析几何) 题型：013
已知抛物线y2＝4x上两个动点B、C和点A(1，2)，且∠BAC＝90°，则动直线BC必过定点
A．(2，5)
B．(－2，5)
C．(5，－2)
D．(5，2)
科目：高中数学 来源：2008全国100所名校最新高考数学 模拟卷(第四套) 题型：013
(理)已知抛物线y2＝4x上两个动点B、C和点A(1，2)且∠BAC＝90°，则动直线BC必过定点
A．(2，5)
B．(－2，5)
C．(5，－2)
D．(5，2)
科目：高中数学 来源：山东省期末题 题型：解答题
x的焦点，离心率是
恒为常数？若存在，求出点M的坐标；若不存在，请说明理由．科目：高中数学 来源：河南省卢氏一高2012届高三上期期末调研考试数学文科试题 题型：044
已知椭圆E的长轴的一个端点是抛物线y2＝4
x的焦点，离心率是
(1)求椭圆E的方程；
(2)过点C(－1，0)，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使
·
为常数？若存在，求出点M的坐标；若不存在，请说明理由．
科目：高中数学 来源：河南省卢氏一高2012届高三上期期末调研考试数学理科试题 题型：044
已知椭圆E的长轴的一个端点是抛物线y2＝4
x的焦点，离心率是
(1)求椭圆E的方程；
(2)过点C(－1，0)，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使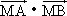
为常数？若存在，求出点M的坐标；若不存在，请说明理由．
科目：高中数学 来源：山东省郓城一中2012届高三上学期寒假作业数学试卷(10) 题型：044
已知椭圆E的长轴的一个端点是抛物线y2＝4
x的焦点，离心率是
(1)求椭圆E的方程；
(2)过点C(－1，0)，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使
·
为常数？若存在，求出点M的坐标；若不存在，请说明理由．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com