练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）=sin（x+），g（x）=cosx（x-），设h（x）=f（x）g（x），则下列说法不正确的是

    A.x∈R，f（x+）=g（x）
    B.x∈R，
    C.x∈R，h（-x）=h（x）
    D.x∈R，h（x+π）=h（x）
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：专项题 题型：单选题

    已知函数f（x）=sin（x+），g（x）=cosx（x-），设h（x）=f（x）g（x），则下列说法不正确的是
    [     ]
    A.x∈R，f（x+）=g（x）
    B.x∈R，
    C.x∈R，h（-x）=h（x）
    D.x∈R，h（x+π）=h（x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2cosx•sin（x+
    π
    3
    ）-
    		3
    sin2x+sinx•cosx
    （I）求函数f（x）的单调递减区间；
    （II）将函数f（x）的图象向右平移m（m＞0）个单位后得到g（x）的图象，求使函数g（x）为偶函数的m的最小值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知函数f（x）=2cosx•sin（x+
    π
    3
    ）-
    		3
    sin2x+sinx•cosx
    （I）求函数f（x）的单调递减区间；
    （II）将函数f（x）的图象向右平移m（m＞0）个单位后得到g（x）的图象，求使函数g（x）为偶函数的m的最小值．

    查看答案和解析>>

    科目：高中数学 来源：0103 期中题 题型：解答题

    已知函数f（x）=2cosx·sin（x+）-sin2x+sinx·cosx。
    （Ⅰ）求函数f(x)的单调递减区间；
    （Ⅱ）将函数f(x)的图象向右平移个单位后得到g(x)的图象，求使函数g(x)为偶函数的的最小正值。

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省梅州市丰顺中学高一（下）第二次月考数学试卷（文科）（解析版） 题型：解答题

    已知函数f（x）=sin（π-x）+cosx
    （1）求f（）；
    （2）求f（x）的值域；
    （3）将函数y=f（x）的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y=g（x）的图象，求函数y=g（x）的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=2cosx•sin(x+
    π
    3
    )-
    		3
    sin2x+sinx•cosx    ．
    （I）求f（x）的值域；
    （II）将函数y=f（x）的图象按向量
    a
    =(
    π
    6
    ，0)    平移后得到函数y=g（x）的图象，求g（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•台州一模）已知向量
    a
    =（sin（x+
    π
    2
    ），sinx），
    b
    =（cosx，-sinx），函数f（x）=m（
    a
    •
    b
    +
    		3
    sin2x），（m为正实数）．
    （1）求函数f（x）的最小正周期及单调递减区间；
    （2）将函数f（x）的图象的纵坐标保持不变，横坐标扩大到原来的两倍，然后再向右平移
    π
    6
    个单位得到y=g（x）的图象，试探讨：当x⊆[0，π]时，函数y=g（x）与y=1的图象的交点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•烟台一模）已知平面向量
    a
    =(cosφ，sinφ)    ，
    b
    =(cosx，sinx)    ，
    c
    =(sinφ，-cosφ)    ，其中0＜φ＜π，且函数f(x)=(
    a
    •
    b
    )cosx+(
    b
    •
    c
    )sinx    的图象过点(
    π
    6
    ，1)    ．
    （1）求φ的值；
    （2）先将函数y=f（x）的图象向左平移
    π
    12
    个单位，然后将得到函数图象上各点的横坐标变为原来的2倍，纵坐标不变，得到函数y=g（x）的图象，求函数y=g（x）在[0，
    π
    2
    ]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省襄阳市襄州、枣阳、宜城、曾都一中联考高三（上）期中数学试卷（理科）（解析版） 题型：解答题

    已知向量=（sin（x+），sinx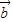），=（cosx，-sinx），函数f（x）=m，（m为正实数）．
    （1）求函数f（x）的最小正周期及单调递减区间；
    （2）将函数f（x）的图象的纵坐标保持不变，横坐标扩大到原来的两倍，然后再向右平移个单位得到y=g（x）的图象，试探讨：当x⊆[0，π]时，函数y=g（x）与y=1的图象的交点个数．

    查看答案和解析>>

    科目：高中数学 来源：2010年浙江省台州市高考数学一模试卷（文科）（解析版） 题型：解答题

    已知向量=（sin（x+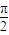），sinx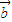），=（cosx，-sinx），函数f（x）=m，（m为正实数）．
    （1）求函数f（x）的最小正周期及单调递减区间；
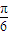    （2）将函数f（x）的图象的纵坐标保持不变，横坐标扩大到原来的两倍，然后再向右平移个单位得到y=g（x）的图象，试探讨：当x⊆[0，π]时，函数y=g（x）与y=1的图象的交点个数．

    查看答案和解析>>


    同步练习册答案