
科目:高中数学 来源: 题型:解答题
已知(x+1)n=a0+a1(x﹣1)+a2(x﹣1)+a3(x﹣1)3+…+an(x﹣1)n,(其中n∈N*)
(1)求a0及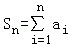 ;
;
(2)试比较Sn与(n﹣2)2n+2n2的大小,并说明理由.
科目:高中数学 来源:吉林省模拟题 题型:解答题
 ||
|| |cos2θ=3,过点B的直线交曲线C于P、Q两点.
|cos2θ=3,过点B的直线交曲线C于P、Q两点.  |+|
|+|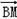 |的值,并写出曲线C的方程;
|的值,并写出曲线C的方程; 科目:高中数学 来源:期末题 题型:解答题
科目:高中数学 来源:不详 题型:解答题
 ;
;科目:高中数学 来源:湖南省月考题 题型:解答题
 ,g(x)=alnx,a
,g(x)=alnx,a R.
R.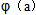 的解析式;
的解析式;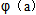 ,证明:当a
,证明:当a (0,+
(0,+ )时,
)时,
 1
1科目:高中数学 来源: 题型:
已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1,记函数f(x)的定义域为D.
(1)求函数f(x)的定义域D;
(2)若函数f(x)的最小值为﹣4,求a的值;
(3)若对于D内的任意实数x,不等式﹣x2+2mx﹣m2+2m<1恒成立,求实数m的取值范围.
科目:高中数学 来源: 题型:
已知函数f(x)=x3+ax2+bx+c,当x=﹣1时,f(x)的极大值为7;当x=3时,f(x)有极小值.求:
(1)a,b,c的值;
(2)函数f(x)的极小值.
科目:高中数学 来源:2013-2014学年河北省保定市高三12月月考理科数学试卷(解析版) 题型:解答题
已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com