
科目:高中数学 来源:不详 题型:单选题
| A.a≤4 | B.a≤3 | C.a≤2 | D.a≥3 |

科目:高中数学 来源:2005-2006学年浙江省温州市高二(上)期末数学试卷(解析版) 题型:选择题

科目:高中数学 来源: 题型:单选题
 如图,已知原点O及点A(1,2),B(a,1),若图中阴影部分(包括边界)上所有的点都在不等式x+y≤4所表示的平面区域内,则实数a的范围是
如图,已知原点O及点A(1,2),B(a,1),若图中阴影部分(包括边界)上所有的点都在不等式x+y≤4所表示的平面区域内,则实数a的范围是科目:高中数学 来源: 题型:
科目:高中数学 来源:2011年新疆乌鲁木齐高级中学高考数学一模试卷(理科)(解析版) 题型:解答题
科目:高中数学 来源:2011年山东省潍坊市高考数学二模试卷(文科)(解析版) 题型:解答题
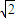 的平行四边形MNEF.平面上的动点G满足|
的平行四边形MNEF.平面上的动点G满足|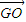 |=2(O为坐标原点)
|=2(O为坐标原点) |∈(
|∈(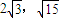 ),求△NPQ内切圆的半径的取值范围.
),求△NPQ内切圆的半径的取值范围.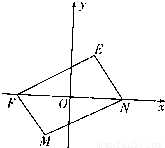
科目:高中数学 来源:2011年山东省潍坊市高考数学二模试卷(理科)(解析版) 题型:解答题
 的平行四边形MNEF.平面上的动点G满足|
的平行四边形MNEF.平面上的动点G满足| |=2(O为坐标原点)
|=2(O为坐标原点) |∈(
|∈( ),求△NPQ内切圆的半径的取值范围.
),求△NPQ内切圆的半径的取值范围.
科目:高中数学 来源: 题型:
 如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).科目:高中数学 来源:2011-2012学年北京市高三下学期开学检测文科数学试卷 题型:解答题
(本小题满分14分)如图,椭圆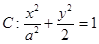 的焦点在x轴上,左右顶点分别为A1,A,上顶点B,抛物线C1,C2分别以A1,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左右顶点分别为A1,A,上顶点B,抛物线C1,C2分别以A1,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线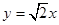 上一点P.
上一点P.
(1)求椭圆C及抛物线C1,C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M,N,已知点 ,求
,求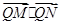 的最小值.
的最小值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com