
科目:初中数学 来源:不详 题型:单选题
| A.SSS | B.ASA | C.AAS | D.SAS |
科目:初中数学 来源:同步题 题型:单选题
科目:初中数学 来源: 题型:解答题
 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由; cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由. 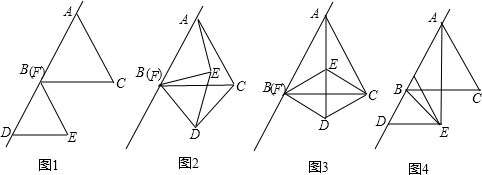
科目:初中数学 来源:2006-2007学年江苏省泰州市兴化市边城中学九年级(上)期中数学试卷(解析版) 题型:解答题
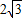 ,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图1中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;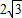 cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由. 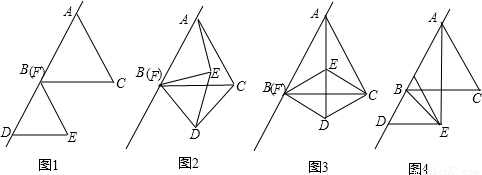
科目:初中数学 来源:边城中学2006-2007年第一学期中学数学试题 题型:059
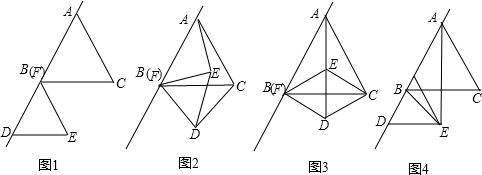
如图1,正△ABC和正△FDE,F与B重合,AB与FD在一条直线上.

(1)若将△FDE绕点B旋转一定角度(如图2),试说明CD=AE;
(2)已知AB=6,DE=![]() ,把图(1)中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
,把图(1)中的△FDE绕点B逆时针方向旋转90°(如图3),试判断四边形EBDC的形状,并说明你的理由;
(3)若把图(1)中的正△FDE沿BA方向平移(如图4),连结AE、BE,已知正△ABC和正△FDE的边长分别是5 cm和![]() cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
cm,问在平移过程中,△ABE是否会成为等腰三角形?若能,直接写出FB的值;若不能,说明理由.
科目:初中数学 来源: 题型:
| 3 |
| 3 |
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 3 |

科目:初中数学 来源:不详 题型:解答题
 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形. ,AC=1+
,AC=1+ ,BC=2,⊙O的直径BE交AC于点D.
,BC=2,⊙O的直径BE交AC于点D.
科目:初中数学 来源: 题型:
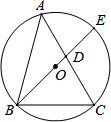 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com