科目：初中数学 来源： 题型：

在等边△ABC的边BA、CB、AC的延长线上，分别截取AA′=BB′=CC′，那么△A′B′C′是（　　）

A、等腰三角形

B、等边三角形

C、任意三角形

D、以上结论都不对

科目：初中数学 来源：不详 题型：单选题

在等边△ABC的边BA、CB、AC的延长线上，分别截取AA′=BB′=CC′，那么△A′B′C′是（　　）

A．等腰三角形	B．等边三角形
C．任意三角形	D．以上结论都不对

查看答案和解析>>

科目：初中数学 来源：《29.1.2 用推理方法研究三角形》2010年同步练习（A卷）（解析版） 题型：选择题

在等边△ABC的边BA、CB、AC的延长线上，分别截取AA′=BB′=CC′，那么△A′B′C′是（）
A．等腰三角形
B．等边三角形
C．任意三角形
D．以上结论都不对

查看答案和解析>>

科目：初中数学 来源： 题型：单选题

在等边△ABC的边BA、CB、AC的延长线上,分别截取AA′=BB′=CC′, 那么△A′B′C′是( )

A.
等腰三角形;
B.
等边三角形;
C.
任意三角形;
D.
以上结论都不对

查看答案和解析>>

科目：初中数学 来源： 题型：单选题

在等边△ABC的边BA、CB、AC的延长线上，分别截取AA′=BB′=CC′，那么△A′B′C′是

A.
等腰三角形
B.
等边三角形
C.
任意三角形
D.
以上结论都不对

查看答案和解析>>

科目：初中数学 来源： 题型：013

在等边△ABC的边BA、CB、AC的延长线上,分别截取AA′=BB′=CC′, 那么△A′B′C′是( )

A．等腰三角形; B．等边三角形; C．任意三角形; D．以上结论都不对

查看答案和解析>>

科目：初中数学 来源：走向清华北大·初二数学 题型：013

如图，在等边△ABC的边BA、CB、AC的延长线上，分别截取＝＝，那么△是

[　　]

A．等腰非等边三角形

B．等边三角形

C．不等边三角形

D．不确定其形状

查看答案和解析>>

科目：初中数学 来源： 题型：

已知△ABC为等边三角形，E为射线BA上一点，D为直线BC上一点，ED=EC．
（1）当点E在AB的上，点D在CB的延长线上时（如图1），求证：AE+AC=CD；
（2）当点E在BA的延长线上，点D在BC上时（如图2），猜想AE、AC和CD的数量关系，并证明你的猜想；
（3）当点E在BA的延长线上，点D在BC的延长线上时（如图3），请直接写出AE、AC和CD的数量关系．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

已知△ABC为等边三角形，E为射线BA上一点，D为直线BC上一点，ED=EC．
（1）当点E在AB的上，点D在CB的延长线上时（如图1），求证：AE+AC=CD；
（2）当点E在BA的延长线上，点D在BC上时（如图2），猜想AE、AC和CD的数量关系，并证明你的猜想；
（3）当点E在BA的延长线上，点D在BC的延长线上时（如图3），请直接写出AE、AC和CD的数量关系．

查看答案和解析>>

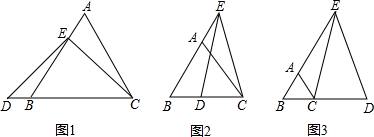
科目：初中数学 来源：2011-2012学年湖北省仙桃市胡场一中九年级（上）期末复习数学试卷（二）（解析版） 题型：解答题

已知△ABC为等边三角形，E为射线BA上一点，D为直线BC上一点，ED=EC．
（1）当点E在AB的上，点D在CB的延长线上时（如图1），求证：AE+AC=CD；
（2）当点E在BA的延长线上，点D在BC上时（如图2），猜想AE、AC和CD的数量关系，并证明你的猜想；
（3）当点E在BA的延长线上，点D在BC的延长线上时（如图3），请直接写出AE、AC和CD的数量关系．

查看答案和解析>>

练习册

高中

初中

小学

在等边△ABC的边BA、CB、AC的延长线上,分别截取AA′=BB′=CC′, 那么△A′B′C′是( )

在等边△ABC的边BA、CB、AC的延长线上，分别截取AA′=BB′=CC′，那么△A′B′C′是