练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中．能组成四点共圆的组数是（　　）
    A．4组B．5组C．6组D．7组
    C
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    1、锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中．能组成四点共圆的组数是（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中．能组成四点共圆的组数是（　　）
    A．4组B．5组C．6组D．7组

    查看答案和解析>>

    科目：初中数学 来源：2000年山西省太原市初中数学竞赛试卷（解析版） 题型：选择题

    锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中．能组成四点共圆的组数是（ ）
    A．4组
    B．5组
    C．6组
    D．7组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    设H为锐角△ABC的三条高AD、BE、CF的交点，若BC=a，AC=b，AB=c，则AH•AD+BH•BE+CH•CF等于（　　）
    A、
    1
    2
    （ab+bc+ca）
    B、
    1
    2
    （a2+b2+c2）
    C、
    2
    3
    （ab+bc+ca）
    D、
    2
    3
    （a2+b2+c2）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    设H为锐角△ABC的三条高AD、BE、CF的交点，若BC=a，AC=b，AB=c，则AH•AD+BH•BE+CH•CF等于（　　）
    A．
    1
    2
    （ab+bc+ca）    		B．
    1
    2
    （a2+b2+c2）    		C．
    2
    3
    （ab+bc+ca）    		D．
    2
    3
    （a2+b2+c2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    设H为锐角△ABC的三条高AD、BE、CF的交点，若BC=a，AC=b，AB=c，则AH•AD+BH•BE+CH•CF等于


    1. A.
      数学公式（ab+bc+ca）
    2. B.
      数学公式（a2+b2+c2）
    3. C.
      数学公式（ab+bc+ca）
    4. D.
      数学公式（a2+b2+c2）

    查看答案和解析>>

    科目：初中数学 来源：2009年黑龙江省哈尔滨市中考数学试题 题型：044

    已知：△ABC的高AD所在直线与高BE所在直线相交于点F．

    (1)如下图，若△ABC为锐角三角形，且∠ABC＝45°，过点F作FG∥BC，交直线AB于点G，求证：FG＋DC＝AD；

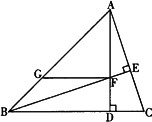
    (2)如下图，若∠ABC＝135°，过点F作FG∥BC，交直线AB于点G，则FG、DC、AD之间满足的数量关系是；

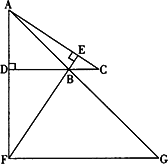
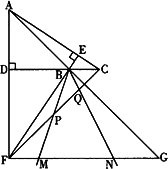
    (3)在(2)的条件下，若AG＝5，DC＝3，将一个45°角的顶点与点B重合并绕点B旋转，这个角的两边分别交线段FG于M、N两点(如下图)，连接CF，线段CF分别与线段BM、线段BN相交于P、Q两点，若NG＝，求线段PQ的长．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：022

    如图所示，锐角三角形ABC的三条高AD、BE、CF交于点H，则△BCH的三条高分别为________．

     

    查看答案和解析>>

    科目：初中数学 来源：同步练习数学　　九年级上册 题型：044

    用尺规作图，并回答问题

    如图所示，已知钝角△ABC．

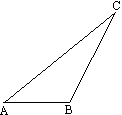
    (1)分别作△ABC三边上的高AD、BE、CF；

    (2)观察AD、BE、CF所在的直线，三条直线是否相交于一点？

    ________________________________________________

    (3)思考：三角形三条高所在直线的交点位置，随三角形的形状各异(锐角三角形、直角三角形、钝角三角形)而有何不同？

    ________________________________________________

    查看答案和解析>>

    科目：初中数学 来源：2010年春季湖北省宜昌市枝江市雅畈中学九年级数学竞赛试卷（解析版） 题型：解答题

    已知：△ABC的高AD所在直线与高BE所在直线相交于点F．
    （1）如图1，若△ABC为锐角三角形，且∠ABC=45°，过点F作FG∥BC，交直线AB于点G，求证：FG+DC=AD；
    （2）如图2，若∠ABC=135°，过点F作FG∥BC，交直线AB于点G，则FG、DC、AD之间满足的数量关系是______；
    （3）在（2）的条件下，若AG=，DC=3，将一个45°角的顶点与点B重合并绕点B旋转，这个角的两边分别交线段FG于M、N两点（如图3），连接CF，线段CF分别与线段BM、线段BN相交于P、Q两点，若NG=，求线段PQ的长．

    查看答案和解析>>


    同步练习册答案