
科目:初中数学 来源: 题型:
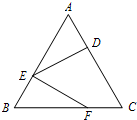 16、如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AE=2EB,EF=ED,∠FED=60°.
16、如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AE=2EB,EF=ED,∠FED=60°.科目:初中数学 来源: 题型:
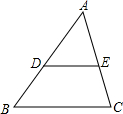 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=| 1 | 2 |
科目:初中数学 来源: 题型:解答题
 如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AE=2EB,EF=ED,∠FED=60°.
如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AE=2EB,EF=ED,∠FED=60°.科目:初中数学 来源: 题型:解答题
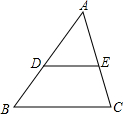 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE= BC.根据上面的结论:
BC.根据上面的结论:科目:初中数学 来源:湖南省期中题 题型:填空题

科目:初中数学 来源: 题型:
如图,在△ABC中,已知∠C=90°,AC=60 cm,AB=100 cm,![]() 、b、c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形
、b、c…是在△ABC内部的矩形,它们的一个顶点在AB上,一组对边分别在AC上或与AC平行,另一组对边分别在BC上或与BC平行.若各矩形在AC上的边长相等,矩形![]() 的一边长是72 cm,则这样的矩形
的一边长是72 cm,则这样的矩形![]() 、b、c…的个数是( )
、b、c…的个数是( )

A.6 B.7 C.8 D.9
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第7期 总第163期 沪科版 题型:044
如图,△
ABC是一块等腰三角形的废铁料(AB=AC).已知∠BAC是锐角,量得底边BC的长为60 cm,BC边上的高为40 cm,用它截一块一边长为30 cm的矩形(要求:使矩形的一边与△ABC的一边重合,而矩形的另两个顶点分别在△ABC的另两条边上).(1)问一共有几种不同的截法,请在图中画出所有截法的示意图,并在图中标明长为30 cm的那条边;
(2)试求出以上你所画的各种截法中,所截得的矩形的另一边长.
科目:初中数学 来源: 题型:
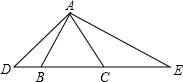 AE=120°,试问:
AE=120°,试问:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com