
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
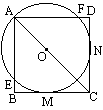
如图,已知O是正方形ABCD对角线AC上一点,以O为圆心,OA的长为半径的圆O与BC相切于M,与AB、AD分别相交于E、F.(1)求证:CD与⊙O相切;(2)若正方形ABCD的边长为1,求⊙O的半径:(3)对于以点M、E、A、F以及CD与⊙O的切点N为顶点五边形的五条边,从相等关系考虑,你可以得出什么结论?请给出证明.
科目:初中数学 来源:2013年初中毕业升学考试(辽宁铁岭卷)数学(解析版) 题型:解答题
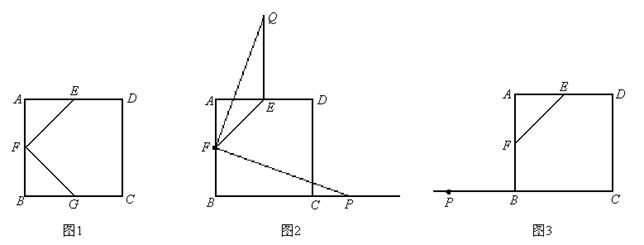
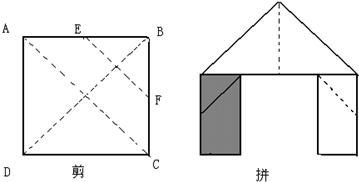
正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.
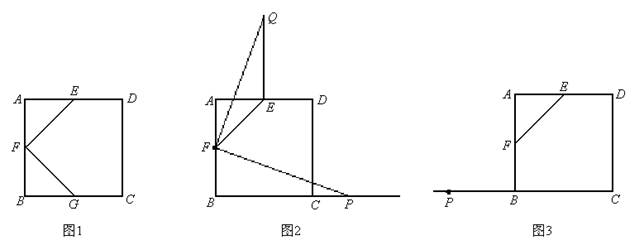
(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
科目:初中数学 来源: 题型:解答题

科目:初中数学 来源:2012年江苏省盐城市解放路学校九年级阶段检测数学试卷(解析版) 题型:解答题
科目:初中数学 来源:不详 题型:解答题
科目:初中数学 来源: 题型:
 PQ.
PQ.科目:初中数学 来源: 题型:
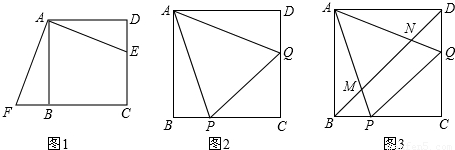
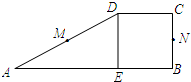 如图,梯形ABCD中,AB∥CD,点M、N分别是AD、BC的中点,DE⊥AB,垂足为点E.若四边形BCDE是正方形,且点M、N关于直线DE对称,则∠DAE的余切值为
如图,梯形ABCD中,AB∥CD,点M、N分别是AD、BC的中点,DE⊥AB,垂足为点E.若四边形BCDE是正方形,且点M、N关于直线DE对称,则∠DAE的余切值为科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
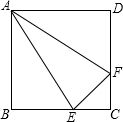 如图,在正方形ABCD中,AB=3,点E、F分别是BC、CD边上的动点,(E、F不与C重合)当EC=CF,且△AEF面积为2.5时,求EF的长.(结果保留根号)
如图,在正方形ABCD中,AB=3,点E、F分别是BC、CD边上的动点,(E、F不与C重合)当EC=CF,且△AEF面积为2.5时,求EF的长.(结果保留根号)科目:初中数学 来源: 题型:
 25、如图,在平行四边形ABCD中,E,F分别是边BC和AD上的点且BE=DF.
25、如图,在平行四边形ABCD中,E,F分别是边BC和AD上的点且BE=DF.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com