
科目:初中数学 来源: 题型:
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法);
(2 矩形ABCD中,AB=3,BC=1,直接写出边CD上A, B两点的勾股点的个数
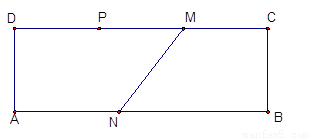
(3 如图2,矩形ABCD中,AB=12,BC=4,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M,N两点的勾股点,且点H在直线l上.求PH的长.
【解析】(1)以线段AB为直径的圆与线段CD的交点,或线段CD的中点;
(2)利用(1)中图形得出C,D,E,F即可得出答案;
(3)求出MN的长度,根据勾股数的特点得出符合要求的点
科目:初中数学 来源:2012届浙江省九年级下学期3月考数学卷(解析版) 题型:解答题
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法);
(2 矩形ABCD中,AB=3,BC=1,直接写出边CD上A, B两点的勾股点的个数
(3 如图2,矩形ABCD中,AB=12,BC=4,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M,N两点的勾股点,且点H在直线l上.求PH的长.
【解析】(1)以线段AB为直径的圆与线段CD的交点,或线段CD的中点;
(2)利用(1)中图形得出C,D,E,F即可得出答案;
(3)求出MN的长度,根据勾股数的特点得出符合要求的点
科目:初中数学 来源: 题型:
 24、如图,在Rt△ABC中,∠C=90°,
24、如图,在Rt△ABC中,∠C=90°,科目:初中数学 来源: 题型:解答题
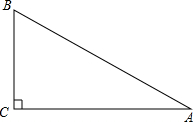 如图,在Rt△ABC中,∠C=90°,
如图,在Rt△ABC中,∠C=90°,科目:初中数学 来源:2009-2010学年江苏省泰州市泰兴市济川实验初中九年级(上)期中数学试卷(解析版) 题型:解答题

科目:初中数学 来源:2009-2010学年江苏省泰州市泰兴市济川实验初中九年级(上)段考数学试卷A(解析版) 题型:解答题

科目:初中数学 来源: 题型:

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com