
科目:初中数学 来源: 题型:
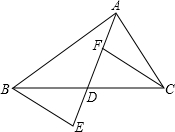 如图,在△ABC中,AB>AC,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.
如图,在△ABC中,AB>AC,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE.科目:初中数学 来源:2012年河北省唐山市路南区中考数学一模试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:
 如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,联结GD,判断△AGD的形状并证明.
如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,联结GD,判断△AGD的形状并证明.科目:初中数学 来源: 题型:解答题
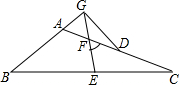 如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,联结GD,判断△AGD的形状并证明.
如图,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,若∠EFC=60°,联结GD,判断△AGD的形状并证明.科目:初中数学 来源:广东省实验中学2010届初中毕业班一模考试数学试题 题型:059
(1)如图,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图,在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.

科目:初中数学 来源: 题型:
 如图:在△ABC中,点D是BC的中点,点E、F分别在AB、AC边上,且DE⊥DF.
如图:在△ABC中,点D是BC的中点,点E、F分别在AB、AC边上,且DE⊥DF.科目:初中数学 来源: 题型:解答题
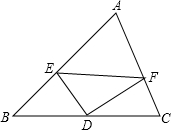 如图:在△ABC中,点D是BC的中点,点E、F分别在AB、AC边上,且DE⊥DF.
如图:在△ABC中,点D是BC的中点,点E、F分别在AB、AC边上,且DE⊥DF.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com