练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    DE为△ABC中平行于AC的中位线，F为DE中点，延长AF交BC于G，则△ABG与△ACG的面积比为（　　）
    A．1：2B．2：3C．3：5D．4：7
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    2、DE为△ABC中平行于AC的中位线，F为DE中点，延长AF交BC于G，则△ABG与△ACG的面积比为（　　）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    DE为△ABC中平行于AC的中位线，F为DE中点，延长AF交BC于G，则△ABG与△ACG的面积比为（　　）
    A．1：2B．2：3C．3：5D．4：7

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    DE为△ABC中平行于AC的中位线，F为DE中点，延长AF交BC于G，则△ABG与△ACG的面积比为


    1. A.
      1：2
    2. B.
      2：3
    3. C.
      3：5
    4. D.
      4：7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在Rt△ABC中，∠BAC=90°，AB=80，BC=100．线段BC所在的直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行，交AB于点D，交AC于点E．解答下列问题：
    （1）求AC的长．
    （2）记x秒时，该直线在△ABC内的部分DE的长度为y，试求出y关于x的函数关系式，并写出自变量x的取值范围．
    （3）如图2，过点D作DG⊥BC于点G，过点E作EF⊥BC于点F，当x为何值时，矩形DEFG的面积最大，最大值是多少？
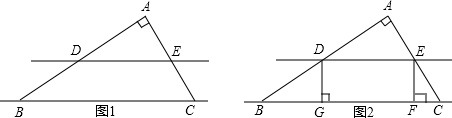
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图1，在Rt△ABC中，∠BAC=90°，AB=80，BC=100．线段BC所在的直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行，交AB于点D，交AC于点E．解答下列问题：
    （1）求AC的长．
    （2）记x秒时，该直线在△ABC内的部分DE的长度为y，试求出y关于x的函数关系式，并写出自变量x的取值范围．
    （3）如图2，过点D作DG⊥BC于点G，过点E作EF⊥BC于点F，当x为何值时，矩形DEFG的面积最大，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年福建省泉州市安溪县恒兴中学九年级（上）期中数学试卷（解析版） 题型：解答题

    如图1，在Rt△ABC中，∠BAC=90°，AB=80，BC=100．线段BC所在的直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行，交AB于点D，交AC于点E．解答下列问题：
    （1）求AC的长．
    （2）记x秒时，该直线在△ABC内的部分DE的长度为y，试求出y关于x的函数关系式，并写出自变量x的取值范围．
    （3）如图2，过点D作DG⊥BC于点G，过点E作EF⊥BC于点F，当x为何值时，矩形DEFG的面积最大，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源：2008-2009学年福建省泉州市师院附属鹏峰中学九年级（上）期中数学试卷（解析版） 题型：解答题

    如图1，在Rt△ABC中，∠BAC=90°，AB=80，BC=100．线段BC所在的直线以每秒2个单位的速度沿BA方向运动，并始终保持与原位置平行，交AB于点D，交AC于点E．解答下列问题：
    （1）求AC的长．
    （2）记x秒时，该直线在△ABC内的部分DE的长度为y，试求出y关于x的函数关系式，并写出自变量x的取值范围．
    （3）如图2，过点D作DG⊥BC于点G，过点E作EF⊥BC于点F，当x为何值时，矩形DEFG的面积最大，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图，在△ABC中，AB=AC，D是底边BC上的一点，过点D作BC的垂线，交AB于点E，交AC的延长线于F，则△AEF是等腰三角形．请在解答过程中的括号里填写理由．
    解：作AH⊥BC于H
    ∵AB=AC（已知）
    ∴∠1=∠2
    （等腰三角形三线合一）
    （等腰三角形三线合一）

    ∵DF⊥BC（已知）
    ∴AH∥DF（平面内垂直于同一条直线的两直线平行）
    ∴∠1=∠F
    （两直线平行，同位角相等）
    （两直线平行，同位角相等）

    ∠2=∠3
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）

    ∴∠F=∠3（等量代换）
    ∴AE=AF
    （等角对等边）
    （等角对等边）

    ∴△AEF是等腰三角形．
    （2）如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=36°，求∠D的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

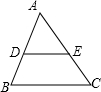    精英家教网在八年级上册我们已经知道三角形的中位线具有如下性质：
    三角形的中位线平行于第三边，并且等于它的一半．
    如图所示，已知△ABC和下列四种说法：
    ①D是AB中点；②E是AC中点；③DE=
    12
    BC；④DE∥BC．
    请你以其中的两种说法为条件（①和②不能同时作为条件），其余两种说法为结论，构造一个命题；并判定你所构造的命题是否正确．如果正确请说明理由；如果不正确，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    23、（12分）在直角三角形ABC中，角A=90度，AB=8，AC=6，若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒钟2个单位长度，过点D作DE平行于BC交于E，设动点D运动的时间为x秒，AE的长为y。

    1.(1)求y与x之间的函数关系式，并写出自变量x的取值范围

    2.（2）求出△BDE的面积S与x之间的函数关系式；

    3.（3）当x为何值时，△BDE的面积S有最大值，最大值为多少？

     

    查看答案和解析>>


    同步练习册答案