
科目:初中数学 来源:不详 题型:单选题
| A.20cm2 | B.30cm2 | C.40cm2 | D.50cm2 |
科目:初中数学 来源: 题型:
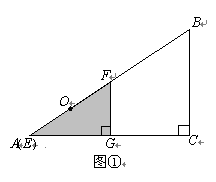

科目:初中数学 来源:2011年江苏省宜兴市九年级上学期期中考试数学卷 题型:解答题
如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC ?
(2)求y与x 之间的函数关系式,并确定自变量x的取值范围.
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142 =12996,1152 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)
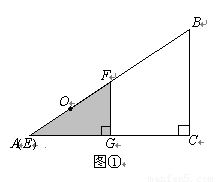

科目:初中数学 来源: 题型:
如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点![]() F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s
F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s![]() ),FG的延长线交 AC于H,(不考虑点P与G、F重合的情况).
),FG的延长线交 AC于H,(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC ?
(2)你能不能用含x的式子来表示四边形OAHP面积呢?若能,请表示;若不能,请说明理由。
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142 =12996,1152 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)
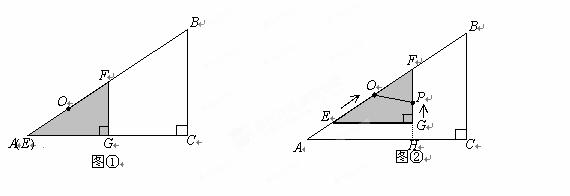
科目:初中数学 来源: 题型:
如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
(1)当x为何值时,OP∥AC ?
(2)求y与x 之间的函数关系式,并确定自变量x的取值范围.
(3)是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142 =12996,115![]() 2 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)
2 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)
 | |||
 | |||
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com