
科目:初中数学 来源: 题型:
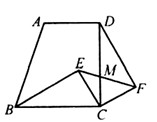
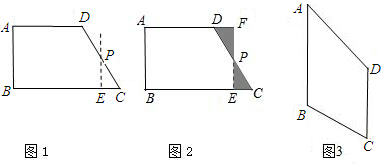
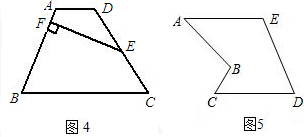
 16、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是
16、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是科目:初中数学 来源:2009-2010学年江西省南昌市师大附中九年级(上)月考数学试卷(12月份)(解析版) 题型:填空题
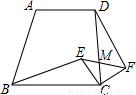
科目:初中数学 来源: 题型:填空题
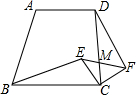 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是________.
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是________.科目:初中数学 来源:江西省月考题 题型:填空题
科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,将一个下底为3,上底为1,且底角为45°的等腰梯形ABCD放置在直角坐标系中,一条动直线x=t从点A开始自左向右匀速运动,至B点处停止运动,它扫过的梯形面积为S(图中阴影部分).
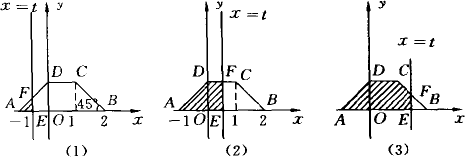
(1)求出梯形ABCD各顶点的坐标;
(2)求过B,C两点的直线解析式;
(3)求出S关于t的函数关系式(从三种情况去考虑:①-1≤t≤0,②0<t≤1,③1<t≤2).
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com