
科目:初中数学 来源: 题型:
 数轴上的点A、B、C、D、O分别表示-1
数轴上的点A、B、C、D、O分别表示-1| 1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源: 题型:
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在![]() 轴上.
轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1(所画△OA1B1与△OAB在原点两侧).
(2)求∠AOB的度数.(结果精确到度)
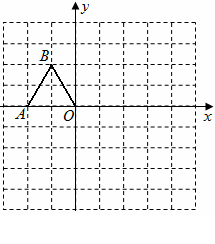 |
科目:初中数学 来源: 题型:
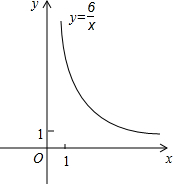 (2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线y=
(2011•西城区模拟)如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线y=| 6 |
| x |
| x | … | … | |||||
| y | … | … |
| S△P1CB |
| S△P1AD |
科目:初中数学 来源: 题型:解答题
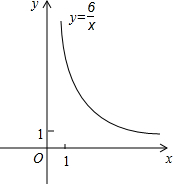 如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线
如图,平面直角坐标系xOy中,点pn(xn,yn)在双曲线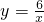 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点. | x | … | … | |||||
| y | … | … |
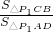 值.
值.科目:初中数学 来源:2011年北京市西城区(北区)初三毕业考试数学试卷(解析版) 题型:解答题
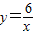 上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点.
上(n,xn,yn都是正整数,且x1<x2<x3<…<xn).抛物线y=ax2+bx+c经过(0,3),(-2,3),(1,0)三点. | x | … | … | |||||
| y | … | … |
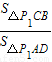 值.
值.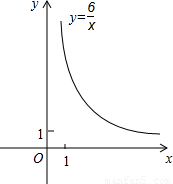
科目:初中数学 来源: 题型:
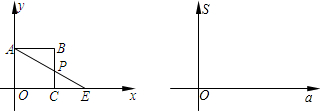 请求出此值;若变化,请说明理由.
请求出此值;若变化,请说明理由.科目:初中数学 来源: 题型:阅读理解
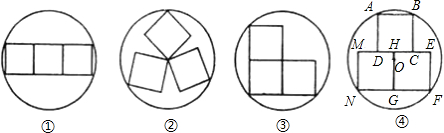
科目:初中数学 来源: 题型:解答题
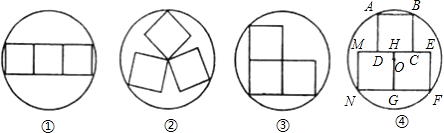
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com