如图所示的四个图形，可以折叠成棱柱的是

1. A.
   
2. B.
   
3. C.
   
4. D.
   

如图所示，四个图形经过折叠可以围成一个棱柱的是

1. A.
   ①②
2. B.
   ②③
3. C.
   ②④
4. D.
   ①③

西湖龙井茶名扬中外．小叶是某龙井茶叶有限公司产品包装部门的设计师．
如图1是用矩形厚纸片（厚度不计）做长方体茶叶包装盒的示意图，阴影部分是裁剪掉的部分．沿图中实线折叠做成的长方体纸盒的上下底面是正方形，有三处矩形形状的“接口”用来折叠后粘贴或封盖．
（1）小叶用长40cm，宽34cm的矩形厚纸片，恰好能做成一个符合要求的包装盒，盒高是盒底边长的2.5倍，三处“接口”的宽度相等．则该茶叶盒的容积是多少？
（2）如图2是小叶设计出的一款茶叶包装，它的里面是由四个圆柱体茶叶罐包装而成的龙井茶．现有一张60cm×44cm的矩形厚纸片，按如图3所示的方法设计包装盒，用来包装四个圆柱体茶叶罐，已知该种的茶叶罐高是底面直径1.5倍，要求包装盒“接口”的宽度为2cm（如有多余可裁剪），问这样的茶叶罐底面直径最大可以为多少？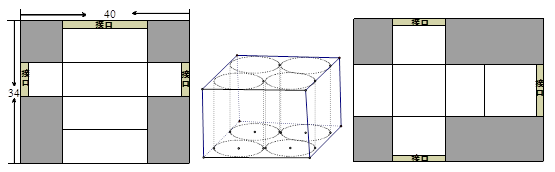                                               

图1                   图2                        图3