练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知点A（5，3），AB垂直于x轴，垂足为B，则B点坐标为（　　）
    A．（0，0）B．（5，0）C．（0，3）D．（3，0）
    B
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    已知等腰△ABC的周长为10，若设腰长为x，则x的取值范围是
     
    ；已知点A是反比例函数y=-
    3x
    图象上的一点．若AB垂直于y轴，垂足为B，则△AOB的面积=
     
    ；若一元二次方程x2-2x-k=0无实数根，则二次函数y=x2+（k+1）x+k的图象最低点在第
     
    象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知二次函数y=mx2+（m-3）x-3  （m＞0）
    （1）求证：它的图象与x轴必有两个不同的交点；
    （2）这条抛物线与x轴交于A（x1，0）和B（x2，0）（x1＜x2），与y轴交于点C，且AB=4，⊙M过A、B、C三点，求扇形MAC的面积S；
    （3）在（2）的条件下，抛物线上是否存在点P使△PBD（PD垂直于x轴，垂足为D）被直线BC分成面积比为1：2的两部分？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011年四川省泸州市江阳区西路学校中考数学查漏补缺试卷（解析版） 题型：解答题

    已知二次函数y=mx2+（m-3）x-3  （m＞0）
    （1）求证：它的图象与x轴必有两个不同的交点；
    （2）这条抛物线与x轴交于A（x1，0）和B（x2，0）（x1＜x2），与y轴交于点C，且AB=4，⊙M过A、B、C三点，求扇形MAC的面积S；
    （3）在（2）的条件下，抛物线上是否存在点P使△PBD（PD垂直于x轴，垂足为D）被直线BC分成面积比为1：2的两部分？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知等腰△ABC的周长为10，若设腰长为x，则x的取值范围是______；已知点A是反比例函数y=-
    3
    x
    图象上的一点．若AB垂直于y轴，垂足为B，则△AOB的面积=______；若一元二次方程x2-2x-k=0无实数根，则二次函数y=x2+（k+1）x+k的图象最低点在第______象限．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年冀教版九年级（上）期末数学水平测试卷（二）（解析版） 题型：解答题

    已知变量y与x成反比例，它的图象过点A（-2，3）．求：
    （1）反比例函数解析式
    （2）从A（-2，3）向x轴和y轴分别作垂线AB、AC，垂足分别为B、C，则矩形OBAC的面积为______．
    （3）当A点的横坐标为-4时，作AB1、AC1分别垂直于x轴、y轴，B1、C1为垂足，则所得矩形OB1AC1的面积是______．
    （4）将A点在图象上任意移动到点A′，作A′B′、A′C′分别垂直于x轴、y轴，B′、C′为垂足，则所得矩形OB′A′C′的面积是______．
    由此，你可以结合上述信息得出结论是：______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （1）阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值．
    对于任意正实数a、b，可作如下变形a+b=(
    		a
    )2+(
    		b
    )2    =(
    		a
    )2+(
    		b
    )2    -2
    		ab
    +2
    		ab
    =(
    		a
    -
    		b
    )2    +2
    		ab
    ，
    又∵(
    		a
    -
    		b
    )2    ≥0，∴(
    		a
    -
    		b
    )2    +2
    		ab
    ≥0+2
    		ab
    ，即a+b≥2
    		ab
    ．
    根据上述内容，回答下列问题：在a+b≥2
    		ab
    （a、b均为正实数）中，若ab为定值p，则a+b≥2
    		p
    ，当且仅当a、b满足
     
    时，a+b有最小值2
    		p
    ．
    （2）思考验证：如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，CO为AB边上中线，AD=2a，DB=2b，试根据图形验证a+b≥2
    		ab
    成立，并指出等号成立时的条件．
    （3）探索应用：如图2，已知A为反比例函数y=
    4
    x
    的图象上一点，A点的横坐标为1，将一块三角板的直角顶点放在A处旋转，保持两直角边始终与x轴交于两点D、E，F（0，-3）为y轴上一点，连接DF、EF，求四边形ADFE面积的最小值．
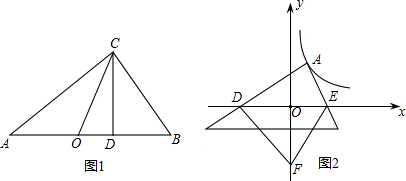
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知如图，直线y=-2x+2与x轴、y轴分别交于点A、B，以线段AB为直角边在第一象限内作等精英家教网腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
    （1）求点A、B的坐标和AD的长；
    （2）求过B、A、D三点的抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知点A（5，3），AB垂直于x轴，垂足为B，则B点坐标为（　　）

    查看答案和解析>>

    科目：初中数学 来源：2013年江苏省苏州高新区中考数学模拟试卷（3月份）（解析版） 题型：解答题

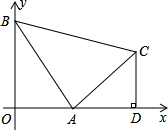
    已知点A（1，c）和点B（3，d）是直线y=k1x+b与双曲线（k2＞0）的交点．
    （1）过点A作AM⊥x轴，垂足为M，连接BM．若AM=BM，求点B的坐标．
    （2）若点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线（k2＞0）于点N．当取最大值时，有PN=，求此时双曲线的解析式．

    查看答案和解析>>

    科目：初中数学 来源：2012年福建省厦门市中考数学试卷（解析版） 题型：解答题

    已知点A（1，c）和点B（3，d）是直线y=k1x+b与双曲线（k2＞0）的交点．
    （1）过点A作AM⊥x轴，垂足为M，连接BM．若AM=BM，求点B的坐标．
    （2）若点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线（k2＞0）于点N．当取最大值时，有PN=，求此时双曲线的解析式．

    查看答案和解析>>


    同步练习册答案